Boule de glu
En physique des particules, une boule de glu, ou glueball en anglais, est une particule composite hypothétique[1]. Elle serait constituée uniquement de gluons sans quarks de valence. Un tel état est possible car les gluons sont porteurs d'une charge de couleur et soumis à l'interaction forte. Comme elles se mélangent avec les mésons ordinaires, les boules de glu sont extrêmement difficiles à identifier au sein des accélérateurs de particules[2].
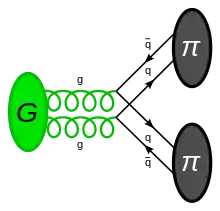
Les calculs théoriques montrent que des boules de glu devraient se former à des énergies accessibles avec les collisionneurs actuels. Cependant, à cause — entre autres — des difficultés mentionnées, elles n'ont à ce jour (2013) toujours pas été observées et identifiées avec certitude[3]. La prédiction de l'existence des boules de glu est l'une des plus importantes prédictions du modèle standard de la physique des particules qui n'a pas encore été confirmée expérimentalement[4].
Propriétés des boules de glu
En principe, il est possible de calculer exactement toutes les propriétés des boules de glu, directement à partir des équations et des constantes fondamentales de la chromodynamique quantique (CDQ) sans avoir à mesurer de nouvelles valeurs. Les propriétés supposées de ces particules hypothétiques peuvent être décrites avec un luxe de détails en utilisant le modèle standard, modèle qui bénéficie d'une large acceptation au sein de la physique théorique. En pratique cependant, les calculs de CDQ sont si complexes qu'on a toujours recours à des approximations numériques pour en déterminer les solutions (avec des méthodes très différentes). De plus les incertitudes considérables sur les mesures de certaines constantes physiques clés peuvent mener à des variations dans les prédictions théoriques des propriétés des boules de glu telles que leur masse, leur rapport de branchement ou leur désintégration.
Particules constitutives et charge de couleur
Les études théoriques des boules de glu se sont concentrées sur les boules composées de deux ou trois gluons par analogie avec les mésons et les baryons qui ont respectivement deux et trois quarks. Comme les mésons et les baryons, les boules de glu seraient neutres de couleur (c'est-à-dire d'isospin nul). Le nombre baryonique d'une boule de glu est 0.
Spin : Moment angulaire total
Les boules de glu à deux gluons peuvent avoir un spin (J) de 0 (ce sont alors des scalaires ou des pseudo scalaires) ou de 2 (tenseurs). Les boules de glu à trois gluons peuvent avoir un spin (J) de 1 (boson vecteur) ou 3. Toutes les boules de glu ont des spins entiers ce qui signifie que ce sont des bosons.
Les boules de glu sont les seules particules prédites par le modèle standard avec un spin de 2 ou 3 dans leur état fondamental bien que des mésons faits de deux quarks avec J=0 et J=1 et des masses similaires ont été observés et des états excités d'autres mésons peuvent avoir une telle valeur de spin.
Des particules fondamentales avec un fondamental de spin 0 ou 2 sont faciles à distinguer d'une boule de glu. L'hypothétique graviton, bien qu'ayant un spin de 2 serait de masse nulle et dénué de charge de couleur le rendant aisément distinguable. Le boson de Higgs pour lequel une masse d'environ 125-126 GeV/c2 a été expérimentalement mesurée (bien que la particule observée n'a pas encore été définitivement identifiée comme un boson de Higgs) est la seule particule fondamentale de spin 0 dans le modèle standard, elle n'a pas non plus de charge de couleur et n'est donc pas soumise à l'interaction forte. Le boson de Higgs a en outre une masse 25 à 80 fois plus importante que les différentes boules de glu prédites par le modèle.
Charge électrique
Toutes les boules de glu ont une charge électrique nulle puisque les gluons eux-mêmes n'ont pas de charge électrique.
Masse et parité
La chromodynamique quantique prédit des boules de glu massives, bien que les gluons eux-mêmes soient de masse nulle au repos dans le modèle standard. Des boules de glu avec les quatre combinaisons possibles de nombres quantiques P (parité) et C (parité C (en)) pour chaque moment angulaire total (J) ont été considérées produisant ainsi une quinzaine d'états possibles pour les boules de glu incluant les états excités ayant des nombres quantiques similaires mais des masses différentes. Les états les plus légers auraient des masses aussi faibles que 1,4 GeV/c2 (boule de glu d'état quantique J=0, P=+, C=+), et les plus lourdes atteindraient 5 GeV/c2 (état quantique J=0, P=+, C=-)[5].
Ces masses sont du même ordre de grandeur que celles de nombreuses particules observées expérimentalement : mésons, baryons, lepton tau, quark charm, quark bottom et certains isotopes de l'hydrogène ou de l'hélium.
Stabilité et mode de désintégration
À l'instar de tous les mésons et baryons du modèle standard, à l'exception du proton, toutes les boules de glu prédites seraient instables lorsqu'elles sont isolées. Différents calculs de chromodynamique quantique prédisent les largeurs de décroissances totales (une quantité liée à la demi-vie) pour différents états des boules de glu. Ces calculs font aussi des prédictions sur les motifs de décroissances[6] - [7]. Par exemple, les boules de glu ne peuvent pas se désintégrer par radiation ou en émettant deux photons, mais pourraient se désintégrer en émettant une paire de pions, une paire de kaons ou une paire de mésons êta[6].
Impact sur la physique macroscopique des basses énergies
Comme les boules de glu prédites par le modèle standard sont extrêmement éphémères (elles se désintègrent presque immédiatement en des produits plus stables) et ne sont générées que dans une physique des hautes énergies, les boules de glu ne peuvent être produites que synthétiquement dans des conditions aisément observables sur Terre. Elles sont donc scientifiquement importantes car elles fournissent une prédiction vérifiable du modèle standard et non pas pour leur impact sur les processus macroscopiques.
Simulations de chromodynamique sur réseau
La théorie des champs sur réseau (en) fournit une méthode pour étudier théoriquement le spectre des boules de glu à partir des principes fondamentaux. Certaines des premières quantités calculées en utilisant les techniques de chromodynamique quantique sur réseau (en 1980) étaient des estimations de la masses des boules de glu[8]. Morningstar et Peardon[9] calculèrent en 1999 la masse des boules de glu les plus légères sans quark dynamique. Les trois états les plus légers sont donnés ci-dessous. La présence de quarks dynamiques modifierait légèrement ces valeurs mais rendrait les calculs plus difficiles encore. Depuis, les calculs de chromodynamique (sur réseau avec règles additives) ont trouvé que les boules de glu les plus légères sont des scalaires de masses comprises entre 1 000 et 1 700 MeV[10].
Candidats expérimentaux
Les expériences menées sur des accélérateurs de particules sont souvent capables d'identifier des particules composites instables et de leur attribuer une masse avec une précision de l'ordre du MeV/c2 sans pour autant être capables de déterminer immédiatement toutes les propriétés correspondantes à la résonance observée. Si les particules détectées dans certaines expériences sont indubitables, d'autres restent encore hypothétiques. Certaines de ces particules candidates pourraient être des boules de glu bien que les preuves ne soient pas irréfutables. On compte notamment :
- X(3020) observées par la collaboration BaBar pourraient être une boule de glu d'état 2-+, 1+- ou 1-- avec une masse autour de 3,02 GeV/c2[4].
- f0(500)/σ -- les propriétés de cette particule pourraient être celles d'une boule de glu de masse entre 1 000 et 1 500 MeV/c2[11].
- f0(980) -- la structure de cette particule composite est en adéquation avec l'existence d'une boule de glu légère[11].
- f0(1370) -- l'existence de cette résonance est discutée, mais elle pourrait être une candidate pour une boule de glu-méson d'états mélangés[11].
- f0(1500) -- l'existence de cette résonance est largement acceptée, mais sa validation comme boule de glu-méson d'états mélangés ou pure n'est pas fermement établie[11].
- f0(1710) -- l'existence de cette résonance est largement acceptée, mais sa validation comme boule de glu-méson d'états mélangés ou pure n'est pas fermement établie[11].
- Les jets de gluons de l'expérience du LEP sont en excès de clusters électromagnétiques neutres de 40 % par rapport aux prédictions théoriques ce qui suggère que des particules électromagnétiques neutres attendues dans des environnements riches en gluons telles que les boules de glu pourraient y être présentes[11].
Nombre de ces candidats font le sujet de recherches actives depuis le milieu des années 1990[6]. L'expérience GlueX (en), prévues pour 2014, a été conçue pour produire des preuves expérimentales définitives sur l'existence des boules de glu.
Notes et références
- (en) Frank Close et Phillip R. Page, "Glueballs", Scientific American, vol. 279 no 5 () p. 80–85.
- (en) Vincent Mathieu, Nikolai Kochelev et Vicente Vento, « The Physics of Glueballs », International Journal of Modern Physics E (nl), vol. 18, , p. 1-49 (DOI 10.1142/S0218301309012124, arXiv 0810.4453).
- (en) Wolfgang Ochs, "The Status of Glueballs" J.Phys.G: Nuclear and Particle Physics 40, 67 (2013) DOI 10.1088/0954-3899/40/4/043001 lire en ligne[PDF].
- (en) Y.K. Hsiao, C.Q. Geng, "Identifying Glueball at 3.02 GeV in Baryonic B Decays" (Version 2: ) lire en ligne.
- (en) Wolfgang Ochs, "The Status of Glueballs" J.Phys.G: Nuclear and Particle Physics 40, 6 (2013) DOI: 10.1088/0954-3899/40/4/043001 lire en ligne[PDF].
- (en) Walter Taki, "Search for Glueballs" (1996) lire en ligne[PDF].
- (en) See, e. g., Walaa I. Eshraim, Stanislaus Janowski, "Branching ratios of the pseudoscalar glueball with a mass of 2.6 GeV", prepared for Proceedings of Confinement X - Conference on Quark Confinement and the Hadron Spectrum (Munich/Germany, 8-12 October 2012) (pre-print published January 15, 2013) lire en ligne.
- (en) B. Berg. Plaquette-plaquette correlations in the su(2) lattice gauge theory. Phys. Lett., B97:401, 1980.
- (en) Colin J. Morningstar et Mike Peardon, « Glueball spectrum from an anisotropic lattice study », Physical Review D, vol. 60, no 3, , p. 034509 (DOI 10.1103/PhysRevD.60.034509, Bibcode 1999PhRvD..60c4509M, arXiv hep-lat/9901004).
- (en) Wolfgang Ochs, "The status of glueballs" Source: JOURNAL OF PHYSICS G-NUCLEAR AND PARTICLE PHYSICS Volume: 40 Issue: 4 Article Number: 043001 DOI: 10.1088/0954-3899/40/4/043001 Published: APR 2013.
- (en) Wolfgang Ochs, « The status of glueballs », Journal of Physics G (en), vol. 40, no 4, , p. 043001 (DOI 10.1088/0954-3899/40/4/043001, Bibcode 2013JPhG...40d3001O, arXiv 1301.5183).
Voir aussi
Articles connexes
- Gluon
- Méson
- méson exotique (en)
- GlueX (en)
- Théorie de Yang–Mills
- Problèmes non résolus en physique