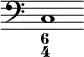Basse chiffrée
La basse chiffrée est une notation musicale composée de chiffres arabes annotant une basse continue[1]. Elle indique les intervalles, accords et notes étrangères pour un morceau de musique improvisé. Ce système était principalement utilisé en musique baroque.

Basse continue
La basse continue a été utilisée tout au long de la période baroque (de 1600 à 1750), principalement sous forme d'une basse chiffrée jouée par le groupe continuo des instruments harmoniques[1]. Le terme « basse continue » provient de l'obligation où se trouvaient les accompagnateurs d'improviser l'accompagnement à partir d'une ligne de basse ininterrompue, même si la voix de basse se taisait. À la fin du XVIe siècle, les organistes ont constitué ainsi des lignes de basse ininterrompues, formées à chaque instant de la note la plus grave chantée par le chœur qu'ils accompagnaient. Le chiffrage de ces basses continues – les chiffres donnant quelques indications sur les accords à réaliser – a donné naissance à la basse chiffrée.
Notation
Une basse chiffrée est constituée d'une partie de basse (notes sur une partition) agrémentée de chiffres et d'altérations placées sous la portée. Ces indications suggèrent les intervalles à jouer, qui correspondent à certains accords ou leurs renversements.
Les compositeurs baroques avaient chacun leur convention de chiffrage. Les chiffres pouvaient même être omis lorsque le compositeur pensait que l'accord à utiliser était évident.

Le chiffrage moderne de la basse peut se résumer ainsi :
- accords de trois notes :
- fondamental : rien ou 5/3
- premier renversement : 6 ou 6/3
- deuxième renversement : 6/4
- accords de quatre notes :
- fondamental : 7
- première renversement : 6/5
- deuxième renversement : 4/3
- troisième renversement : 4/2
Superpositions et inversions


Le principe de base du chiffrement est que la basse est sur l'un ou l'autre degré de la gamme utilisée, noté (quand c'est nécessaire) par un chiffre romain. Cette basse étant donnée, on peut noter (en chiffre arabe) chaque note de l'accord par l'intervalle qu'il réalise avec la basse : 2 pour une seconde, 3 pour une tierce, 6 pour une sixte, etc. Ainsi, dans un ton de Do majeur, un accord de ré mineur serait théoriquement noté (ii-1\3\5), c'est-à-dire à partir du second degré (Ré) jouer l'unisson (Ré) avec la tierce supérieure (Fa) et la quinte (La). Les intervalles ainsi notés sont implicitement majeurs ou mineurs, augmentés ou diminués, en fonction de ce que dit la gamme utilisée.
Dans la théorie harmonique sous-jacente, un accord est conçu comme une succession de tierces (ou éventuellement de quartes), les voix pouvant être déplacées d'une octave sans changer la nature de l'accord. L'accord naturel comprend trois notes, et est réalisé par défaut à partir de la note de basse, l'harmonie étant obtenue en augmentant cette basse par deux tierces successives dans la gamme de départ - la tierce et la quinte. Cette construction étant « par défaut », il est inutile d'en noter les chiffres : en Do majeur, une basse sur un La implique implicitement un accord La-Do-Mi, et la notation théorique 1\3\5 n'a pas besoin d'être explicitée.
La notation d'un chiffre devient nécessaire dans deux cas : quand un accord comprend plus de trois notes, et quand il n'est pas réalisé par une succession de tierces.
Ainsi, dans une gamme de Do majeur, le premier renversement d'un accord de Do part d'une basse de Mi, à laquelle s'ajoute un Sol (une tierce au-dessus) et un Do (une sixte au lieu d'une quinte attendue par défaut). Son chiffrage théorique est donc (iii-1\3\6). Mais ce chiffrage complet donne beaucoup d'information inutile. Le 1 est tautologique, puisque le Mi est à la basse il est nécessairement joué ; et le 3 est implicite dans une harmonie conçue comme des successions de tierces. La seule information réelle est le 6, qui marque qu'il faut jouer la sixte de la basse et non la quinte attendue. Le chiffrage réel se limite donc à (iii-6). De même, le deuxième renversement d'un accord de Do part d'une basse de Sol, auquel est ajouté un Do (4) et un Mi (6). Son chiffrement théorique (v-1\4\6) peut se réduire à (v-4\6), voire simplement à (v-4) puisqu'implicitement l'accord comporte trois notes, la troisième étant à une tierce de la précédente.
L'accord par défaut étant de trois notes, il faut de même indiquer les notes supplémentaires. Un accord de septième dans sa position fondamentale comprendra les degrés (1\3\5\7), et se notera simplement 7 puisque les trois premiers degrés sont implicitement présents, et implicitement sous forme de tierces successives. L'accord de septième, quand la basse est la tonique, est donc simplement noté 7. De même, un accord de treizième, superposant six tierces, sera simplement noté 13, pour traduire la succession de notes 1\3\5\7\0\11\13, implicitement sous forme de tierces successives. Le 13 d'un Fa majeur, dans ce cas, ne signifie pas juste la présence d'un Ré aigü (treizième de la basse), mais bien la superposition des tierces jusqu'à ce Ré aigü. La simple superposition d'un Ré à un accord de Fa majeur (dans la gamme de Fa) correspond simplement à l'ajout d'une sixte, qui peut alors se noter (6/5) sans avoir à évoquer la treizième.
Le premier renversement d'un accord de septième comprend les notes (1\3\5\6), où la notation des deux premiers chiffres n'apporte pas d'information. En revanche, il est nécessaire de noter aussi bien la quinte que la sixte, donc 6/5, pour distinguer cet accord de l'accord 6, premier renversement d'un accord à trois notes. Le deuxième renversement comprend les notes (1\3\4\6), et se note de même 4/3 (le complément à la sixte supérieure étant implicite). Le troisième renversement comprend les notes (1\2\4\6) et son chiffrement peut se limiter à 2, puisque les deux autres tierces doivent être implicitement complétées.
Notes et références
- Abromont 2001, p. 532
Voir aussi
Bibliographie
- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. [détail des éditions] (ISBN 978-2-213-60977-5)