Arbre radix
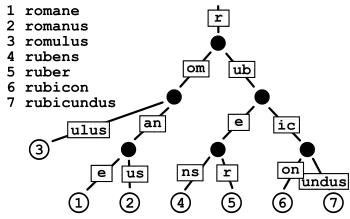
En informatique, un arbre radix ou arbre PATRICIA (pour Practical Algorithm To Retrieve Information Coded In Alphanumeric en anglais et signifiant algorithme commode pour extraire de l'information codée en alphanumérique) est une structure de données compacte permettant de représenter un ensemble de mots adaptée pour la recherche. Il est obtenu à partir d'un arbre préfixe en fusionnant chaque nœud n'ayant qu'un seul fils avec celui-ci. On peut alors étiqueter indifféremment chaque arête par un mot ou bien par une unique lettre.
Histoire
Le premier à parler d’« arbre de PATRICIA » est Donald R. Morrison[1]. À peu près au même moment, Gernot Gwehenberger invente indépendamment la même structure[2].
Applications
Les arbres Patricia peuvent être utilisés dans la construction de tableaux associatifs.
Primitives
- Insertion : Ajout d'un mot à l'arbre.
- Suppression : Suppression d'un mot de l'arbre.
- Recherche : Détermine si un mot est ou non dans l'arbre.
On peut également ajouter d'autres primitives selon les usages :
- Recherche des mots avec un préfixe commun : Détermine la liste des mots commençant par un certain préfixe.
- Recherche du mot précédent : Recherche du plus grand mot parmi ceux plus petits qu'un certain mot. Les comparaisons utilisent l'ordre lexicographique.
- Recherche du mot suivant : Recherche du plus petit mot parmi ceux plus grands qu'un certain mot.
Recherche
Rechercher un mot dans un arbre consiste à parcourir l'arbre de manière que les arêtes parcourues mises bout à bout forment le mot recherché.
Plus précisément, on part de la racine et on regarde si l'une des arêtes est un préfixe du mot. Si on n'en trouve pas, le mot ne se trouve pas dans l'arbre. Sinon, on réitère le processus sur le nœud correspondant, jusqu'à ce que l'on tombe sur une feuille. Lorsqu'on arrive à une feuille, deux cas se présentent : soit le mot correspond aux arêtes parcourues mises bout à bout, soit le mot est en fait plus long et ne fait que commencer par le mot lu sur l'arbre. Dans ce cas, le mot n'est pas contenu dans l'arbre.
Cet algorithme est illustré par le pseudo-code suivant :
Fonction rechercher(arbre,mot) :
Si est_feuille(arbre) et est_vide(mot) alors
Renvoyer Vrai
Sinon si est_vide(mot) ou est_feuille(arbre) alors
Renvoyer Faux
Sinon
Pour arête dans arêtes(arbre) faire
Si est_un_préfixe(arête,mot) alors
Renvoyer rechercher(sous_arbre(arbre,arête) , suffixe(mot,taille(arête)) )
Renvoyer Faux
Suppression
Cette opération se fait à l'identique de la recherche d'un mot. Lorsqu'on a trouvé le mot à supprimer, il suffit ensuite de supprimer la feuille correspondant à l'identique d'une suppression sur un arbre.
Insertion
L'insertion d'un mot commence par le parcours de l'arbre de manière identique à la recherche d'un mot jusqu'à ce qu'aucune des arêtes ne coïncide avec la fin du mot à insérer. Si l'on arrive à une feuille, c'est que le mot est déjà dans l'arbre. Sinon on cherche une arête ayant un préfixe commun avec la suite du mot.
- Si aucune des arêtes n'a de préfixe commun, on ajoute un fils au nœud sur lequel on se trouve. L'arête les reliant est la fin du mot à insérer.
- Sinon, on choisit l'un des préfixes en commun, on supprime l'arête correspondante. On crée ensuite une arête ayant pour étiquette ce préfixe et on lui ajoute deux fils avec pour étiquettes l'une le suffixe de l'arête que l'on a supprimé, l'autre la fin du mot à insérer privée du préfixe commun.
Comparaison avec les autres structures de données
Dans la comparaison suivante, on supposera que les mots sont de longueur k et que le nombre de mot est n.
Les opérations de recherche, de suppression et d'insertion d'un mot ont des complexités en O(k). Par conséquent, la complexité temporelle de ces opérations ne dépend pas du nombre de données contenues par l'arbre radix. Avec un arbre équilibré, cette complexité est en O(ln(n)). Cependant, dans la plupart des cas, k est plus grand que ln(n), sauf dans les cas où la quantité de donnée serait très importante. Malgré tout, les comparaisons dans un arbre équilibré sont des comparaisons de chaînes de caractères qui sont le plus souvent en complexité en O(k).
Bien que la complexité pour un trie soit elle aussi en temps constant par rapport au nombre de données, les opérations demandent exactement m comparaisons pour un mot de longueur m alors que ce nombre peut être diminué dans un arbre radix.
Les arbres radix partagent les désavantages des tries. En effet, ils ne s'appliquent qu'aux chaînes de caractères ou aux éléments pouvant aisément être transformés en chaîne de caractère (et réciproquement) alors que les arbres équilibrés peuvent s'appliquer sur tout ensemble d'éléments muni d'une relation d'ordre total. Les arbres radix ne sont donc pas adaptés aux types de données ne possédant pas d'opération de sérialisation.
Le temps d'insertion et de suppression d'une table de hachage sont souvent considérés comme étant en O(1), mais ce n'est vrai que si l'on considère que le calcul de la clé via la fonction de hachage est en temps constant. En prenant en compte le temps de hachage, la complexité s'avère en fait être en O(k) dans le cas des mots, voire plus si des collisions apparaissent lors du calcul. De plus, ni la fonction de recherche du successeur, ni celle de recherche du prédécesseur ne peuvent être implémentées à l'aide d'une table de hachage.
Variantes
Une variante courante des arbres radix consiste à introduire deux couleurs pour chaque nœud, par exemple "blanc" et "noir". L'algorithme de recherche est alors le même que celui précédemment sauf que si la feuille sur laquelle on arrive est noire, alors le mot recherché n'est pas dans l'arbre. Cela permet d'ajouter plusieurs mots à la fois (par exemple tous les mots ayant un même préfixe) puis d'enlever quelques exceptions en les insérant avec un nœud noir.
Voir aussi
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Radix tree » (voir la liste des auteurs).
- Morrison, Donald R. Practical Algorithm to Retrieve Information Coded in Alphanumeric
- G. Gwehenberger, Anwendung einer binären Verweiskettenmethode beim Aufbau von Listen. Elektronische Rechenanlagen 10 (1968), pp. 223–226