Arbre équilibré
En informatique, un arbre équilibré, aussi appelé arbre à critère d'équilibre, est un arbre qui maintient une profondeur équilibrée entre ses branches. Cela a l'avantage que le nombre de pas pour accéder à la donnée d'une clé est en moyenne minimisé, et ce nombre est égal (+/- 1) quelle que soit la clé.
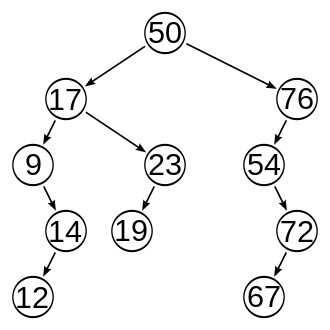
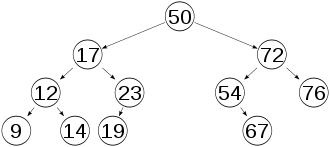
Le but est d'éviter de construire des arbres dits dégénérés (arbres peignes), dans lesquels certains chemins d'accès aux données sont d'une longueur disproportionnée. Cela peut être très avantageux lorsqu'on réutilise l'arbre ainsi construit : en effet, utiliser un arbre équilibré permet d'avoir un temps de recherche de complexité logarithmique dans le pire des cas au lieu d'une complexité linéaire, comme c'est parfois le cas pour des arbres dégénérés.
Arbres binaires de recherche bien équilibrés
Les arbres binaires de recherche présentent des cas de dégénérescence les rendant trop lents dans beaucoup de cas. Une amélioration consiste à ajouter à leurs spécifications un critère d'équilibre imposant des restrictions sur le sous-arbre droit (SAD) et gauche (SAG).
Arbre binaire à critère d'équilibre total
Avec ce type d'arbre, l'arbre doit être complet c'est-à-dire que, si sa profondeur est n, le niveau n-1 est entièrement rempli. Cette approche est très rarement utile, une insertion pouvant demander la réorganisation de l'arbre entier. Insertion et suppression en O(N), recherche en O(log2 N).
Arbre binaire à critère d'équilibre partiel
Dans un arbre AVL, la hauteur du SAG et celle du SAD diffèrent au plus de un. Le nombre maximal de réorganisations est en O(log2 N), c'est-à-dire la hauteur de l'arbre. L'insertion, la recherche et la suppression sont en O(log2 N).
Arbre rouge-noir
Arbre SBB ou arbre rouge-noir : un arbre équilibré où la profondeur maximum de l'arbre est en 2 × log2 (N + 1).
Structure de données similaire
Il existe une structure de donnée hybride qui ressemble à un arbre et dont les feuilles forment une liste chaînée : la skip list. Elle possède aussi un critère d'équilibre ; mais celui-ci est probabiliste, et non déterministe.