Arbre de segments

Cette section décrit la structure d'un arbre segment à 1 dimension.

Soit S l'ensemble d'intervalles, ou segments. Soit p₁, p₂, ..., p_m la liste des points d'extrémités d'intervalle distincts, trié de gauche à droite. On considère le partitionnement de la réelle ligne induite par ces points. Les régions de ce partitionnement sont nommés intervalles élémentaires. Ainsi, les intervalles élémentaires, sont de gauche à droite.

${\displaystyle (-\infty ,p_{1}),[p_{1},p_{1}],(p_{1},p_{2}),[p_{2},p_{2}],...,(p_{m-1},p_{m}),[p_{m},p_{m}],(p_{m},+\infty )}$

Comme cela, la liste des intervalles élémentaires consistent à des intervalles ouverts entre deux points d'extrémités consécutifs p_i et p_i+1, alternés avec des intervalles fermés qui consistent en un seul point d'extrémité. Les points isolés sont traités comme des intervalles car la réponse à une requête n'est pas nécessairement la même à l'intérieur d'un intervalle élémentaire et ses points d'extrémités[2].

Exemple graphique de la structure d'un arbre segment. Cette instance est construite pour les segments montrés en bas.

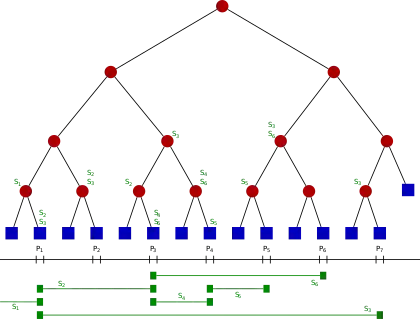
Étant donné un ensemble I d'intervalles, ou segments, un arbre segment T pour I est structuré comme ceci :

• T est un arbre binaire
• Ses feuilles correspondant aux intervalles élémentaires induits par les points d'extrémités dans I, d'une manière ordonnée : la feuille la plus à gauche correspond à l'intervalle le plus à gauche, ainsi de suite. L'intervalle élémentaire correspondant à la feuille v est noté Int(v).
• Les nœuds internes de T correspondent à des intervalles qui sont l'union d'intervalles élémentaires : l'intervalle Int(N) correspondant au nœud N est l'union des intervalles correspondants aux feuilles de l'arbre qui débute à la racine N. Cela implique que Int(N) est l'union des intervalles de ces deux fils (sous-arbres).
• Chaque nœud ou feuille v de T stocke l'intervalle Int(v) ou dans certaines structures de données un ensemble d'intervalles. Ce sous-ensemble canonique de nœuds v contient les intervalles [x, x′] de I de telle manière que [x, x′] contient Int(v) et ne contient pas Int(parent(v)). Cela étant, chaque nœud dans T stocke les segments qui couvrent son intervalle, mais qui ne couvrent pas l'intervalle de son parent[3].

Cette section analyse le coût du stockage d'un arbre segment à 1 dimension.

Un arbre segment T sur un ensemble I de n intervalles utilise un stockage de O(n log n).

Preuve:

Lemma: Tout intervalle [x, x′] de I est stocké dans l'ensemble canonique pour, au maximum, deux nœuds à la même profondeur.

Preuve: Soit v₁, v₂, v₃ trois nœuds à la même profondeur, numérotés de gauche à droite ; et soit p(v) le nœud père de n'importe quel nœud v. Supposons que [x, x′] est stocké à v₁ and v₃. Cela signifie que [x, x′] couvre en entier l'intervalle depuis le point d'extrémité gauche de Int(v₁) jusqu'au point d'extrémité droite de Int(v₃). Remarquons que tous les segments à un niveau particulier ne se chevauchent pas et ordonnés de gauche à droite : par construction, cela est vrai pour le niveau contenant les feuilles, et la propriété n'est pas perdue en allant au niveau au-dessus en combinant par pair les segments adjacents. Maintenant, soit parent(v₂) = parent(v₁), ou c'est celui à droite de ce dernier (les arêtes dans ce graphe ne se croisent pas). Dans le premier cas, le point le plus à gauche de Int(parent(v₂)) est le même que le point le plus à gauche de Int(v₁) ; dans le second cas, le point le plus à gauchede Int(parent(v₂)) est à droite du point le plus à droite de Int(parent(v₁)), et ainsi, aussi à droite du point le plus à droite de Int(v₁). Dans les deux cas, Int(parent(v₂)) débute au niveau, ou à droite, du point le plus à gauche de Int(v₁). Un raisonnement similaire montre que Int(parent(v₂)) se termine au niveau, ou à gauche, du point le plus à droite de Int(v₃). Int(parent(v₂)) doit ainsi être contenu dans [x, x′] ; par conséquent [x, x′] ne sera pas stocké à v₂.

L'ensemble I a au plus 4n + 1 intervalles élémentaires. Car T est un arbre binaire équilibré avec au plus 4n + 1 feuilles, sa hauteur est O(logn). Étant donné qu'un intervalle est au plus stocké deux fois à une certaine profondeur de l'arbre, ainsi le stockage total est O(nlogn)[4].

Cette section décrit la construction d'un arbre segment à 1 dimension.

Un arbre segment à partir de l'ensemble de segments I, peut-être construit comme ceci. Premièrement, les points d'extrémités des intervalles dans I sont triés. les intervalles élémentaires sont obtenus à partir de cela. Ensuite, un arbre binaire équilibré est construit sur les intervalles élémentaires, et pour chaque sommet v l'intervalle Int(v) est déterminé. Il reste à calculer le sous-ensemble canonique pour les nœuds. Pour réussir cela, les intervalles dans I sont insérés un par un dans l'arbre segment. Un intervalle X = [x, x′] peut être inséré dans un sous-arbre enraciné à t, en utilisant la procédure suivante[5] :

• Si Int(T) est contenu dans X alors stocker X à T, et finir.
• Else :
• Si X intersecte l'intervalle du fils gauche de T, alors insérer X dans ce fils, récursivement.
• Si X intersecte l'intervalle du fils droit de T, alors insérer X dans ce fils, récursivement.

L'opération de construction complète nécessite le temps O(nlogn), n étant le nombre de segments dans I.

Preuve

Trier les points d'extrémités prend O(nlogn). Construire un arbre binaire équilibré depuis les points d'extrémités nécessite un temps linéaire en n.

L'insertion d'un intervalle X = [x, x′] dans l'arbre coûte O(logn).

Preuve:Visiter chaque nœud prend un temps constant (en assumant que les sous-ensembles canoniques sont stockés dans une structure de données simple, comme une liste chaînée). Quand on visite un nœud v, soit on stocke X à v, ou Int(v) contient un point d'extrémité de X. Comme prouvé au-dessus, un intervalle est au plus stocké deux fois à chaque niveau de l'arbre. Il y a aussi au plus un nœud à chaque niveau où son intervalle correspondant contient x, et un nœud où son intervalle contient x′. Donc, au plus quatre nœuds par niveau sont visités. Étant donné qu'il y a O(logn) niveaux, le coût total de l'insertion est O(logn)[1].

Cette section décrit l'opération d'une requête dans un arbre segment à 1 dimension.

Une requête pour un arbre segment, reçoit une point q_x (qui devrait être une des feuilles de l'arbre), et retrouve une liste de tous les segments stockés qui contiennent le point q_x.

Formellement énoncé ; en fonction d'un nœud (sous-arbre) v et une requête sur un point q_x, la requête peut être faite en utilisant l'algorithme suivant :

• Signaler tous les intervalles dans I(v)
• Si v n'est pas une feuille :
  • Si q_x est dans Int(fils gauche de v) alors
    • Réaliser une requête dans le fils gauche de v.
  • Si q_x est dans Int(fils droit de v) alors
    • Réaliser une requête dans le fils droit de v.

Si un arbre segment contient n intervalles, ceux qui contiennent un point d'une requête peuvent être signalés en un temps O(logn + k), où k est le nombre d'intervalles signalés.

Proof:L'algorithme de requête visite un nœud par niveau de l'arbre, donc O(logn) nœuds au total. D'un autre côté, à un nœud v, les segments dans I sont signalés en un temps O(1 + k_v), où k_vest le nombre d'intervalles signalés au nœud v. La somme de tous les k_v pour tous les nœuds v visités, est k, le nombre de segments signalés[4].

L'arbre segment peut être généralisé pour des espaces à plus grandes dimensions, dans la forme d'un arbre segment à plusieurs niveaux. Les versions à plus de dimensions, l'arbre segment stocke une collection d'axes-parallèles (hyper-)rectangles, et peut retrouver les rectangles qui contiennent le point d'une certaine requête. La structure utilise un espace de O(nlog^dn) et résout les requêtes en O(log^dn).

L'utilisation de cascade fractionnée diminue la borne du temps de requête par un facteur logarithmique. L'utilisation d'arbre intervalle au niveau le plus profond des structures associées diminue la borne inférieure du stockage par un facteur logarithmique[6].

Une requête qui demande tous les intervalles qui contiennent un certain point est souvent mentionné en anglais comme stabbing query[7].

L'arbre segment est moins efficace que l'arbre intervalle pour les requêtes de distance dans 1 dimension, cela est dû au stockage qui est davantage conséquent : O(nlogn) contre O(n) pour l'arbre d'intervalle. L'importance de l'arbre segment est que les segments dans chaque nœud, son sous-ensemble canonique peut être stocké d'une manière arbitraire[7].

Pour n intervalles où les points d'extrémités sont dans une petite plage de nombres entiers (par exemple, dans la plage [1,...,O(n)]), une structure de donnée optimale existe avec un temps de prétraitement linéaire et un temps de requête de O(1+k) pour signaler tous les k intervalles qui contiennent le point d'une certaine requête.

Un autre avantage de l'arbre segment est qu'il peut être facilement adapté aux requêtes de comptage ; qui est de signaler le nombre de segments qui contiennent un certain point, au lieu de signaler les segments eux-mêmes. À la place de stocker les intervalles dans des sous-ensembles canoniques, on peut simplement stocker le nombre qu'ils sont. Ainsi un arbre linéaire utilise un stockage linéaire, et requiert un temps de requête de O(log n)[8].

Des versions avec de plus grandes dimensions pour l'arbre intervalle et pour les arbres de recherche prioritaies n'existent pas ; cela étant, il n'y a pas d'extension claire de ces structures qui résout le problème analogue dans des dimensions supérieurs. Mais les structures peuvent être utilisés comme structures associées des arbres segments[6].

L'arbre segment a été inventé par Jon Louis Bentley en 1977, dans "Solutions to Klee’s rectangle problems"[7].

• (en) Mark de Berg, Marc van Kreveld, Mark Overmars et Otfried Schwarzkopf, Computational Geometry: algorithms and applications, Springer-Verlag Berlin Heidelberg New York, 2000 (ISBN 3-540-65620-0, DOI 10.1007/978-3-540-77974-2), « More Geometric Data Structures »
• http://www.cs.nthu.edu.tw/~wkhon/ds/ds10/tutorial/tutorial6.pdf