Arbre de Pythagore

L'arbre de Pythagore est une fractale plane construite à l'aide de carrés. Elle porte le nom de Pythagore car chaque triplet de carrés en contact enclot un triangle rectangle, une configuration traditionnellement utilisée pour illustrer le théorème de Pythagore.

L'arbre

Construction

La construction de l'arbre de Pythagore débute avec un simple carré. Sur ce carré sont construits deux autres carrés, dont chaque côté est plus petit d'un facteur ½√2 par rapport au carré de l'étape précédente, tels que les sommets des carrés soient en contact. La procédure est appliquée récursivement à chaque carré, jusqu'à l'infini. L'illustration ci-dessous illustre les premières itérations de la construction.

Construction de l'arbre de Pythagore, ordre 1	Ordre 2	Ordre 3	Ordre 4
Ordre 0	Ordre 1	Ordre 2	Ordre 3

Code pour la construction de l'arbre de Pythagore classique par récursivité

Les coordonnées sont sous la forme abscisse,ordonnée.

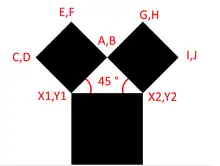
Première itération de l'arbre de Pythagore sous forme classique.

Schéma arbre de Pythagore, angles à 45°

A = (X1 + X2) / 2 - (Y2 - (Y2 + Y1) /2)
B = (Y1 + Y2) / 2 + (X2 - (X2 + X1) /2)
C = X1- (B - Y1)
D = Y1 + (A - X1)
E = A - (B - Y1)
F = B + (A - X1)
G = A - (Y2 - B)
H = B + (X2 - A)
I = X2 - (Y2 - B)
J = Y2 + (X2 - A)

Il suffit de connaître X1, Y1, X2 et Y2 pour pouvoir calculer les autres.

À l'itération suivante, on effectuera ces calculs deux fois : la première fois avec (X1,Y1,X2,Y2) = (C,D,E,F) et la seconde avec (X1,Y1,X2,Y2) = (G,H,I,J).

Aire

La n^e itération ajoute 2ⁿ carrés de côté (½√2)ⁿ, pour une aire totale de 1. Ainsi, l'aire totale de l'arbre semble a priori tendre vers l'infini. Cependant, certains des carrés se superposent à partir de la 5^e itération, l'arbre possède donc une aire finie et tient dans un rectangle de 6×4.

Variations

En conservant la contrainte de former un triangle rectangle à partir de trois carrés, mais en donnant des tailles différentes à chacun des carrés ajoutés à chaque itération, il est possible de créer des formes fractales similaires à l'arbre de Pythagore. L'illustration suivante illustre une telle variation

Ordre 0	Ordre 1	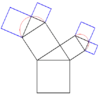Ordre 2	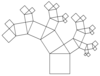Ordre 5
Ordre 0	Ordre 1	Ordre 2	Ordre 5

Code pour la construction de l'arbre de Pythagore avec angles différents de 45°

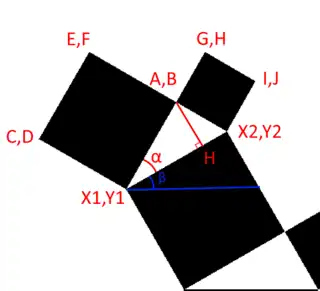
Schéma de la construction de l'arbre de Pythagore, angle différent de 45°

α (alpha) est l'angle que l'on donne au départ, il ne varie jamais. Le triangle est toujours rectangle, mais plus isocèle rectangle comme il l'était dans la forme classique de l'arbre de Pythagore, avec alpha = 45°.

β (beta) est l'angle situé entre le segment [X1Y1X2Y2] et l'horizontale, ici représentée par le trait bleu.

H est le point d'intersection de la droite (X1Y1X2Y2) et de la hauteur h issue de AB. Seul le nom du point est donné car on ne va pas calculer ses coordonnées.

HX1Y1 est la distance entre le point de coordonnées (X1,Y1) et le point H.

ABX1Y1 est la distance entre le point de coordonnées (A,B) et le point de coordonnées (X1,Y1).

Pseudo-code

# On peut utiliser les nombres complexes pour calculer beta
# j le nombre complexe
angle beta = argument du nombre complexe X2 + Y2j - (X1 + Y1j)
distance HX1Y1 = distance X1Y1X2Y2 * cosinus(alpha°)² # voir démonstration plus bas
distance ABX1Y1 = HX1Y1 / cosinus(alpha°) #simple théorème de Pythagore
A = X1 + ABX1Y1 * cos(alpha + beta) # théorème de Pythagore avec le triangle rectangle qui a pour hypoténuse ABX1Y1 et dont un des côtés adjacents est situé sur l'horizontale (sur le trait bleu), et l'autre est donc situé sur la verticale.
B = Y1 + ABX1Y1 * sin(alpha + beta) # même raisonnement
C = X1 - (B - Y1)
D = Y1 + (A - X1)
E = A - (B - Y1)
F = B + (A - X1)
G = A - (Y2 - B)
H = B + (X2 - A)
I = X2 - (Y2 - B)
J = Y2 + (X2 - A)

Démonstration HX1Y1

{\begin{cases}tan(\alpha )=ABH/HX1Y1\\tan(90-\alpha )=ABH/HX2Y2\end{cases}}\Longleftrightarrow {\begin{cases}tan(\alpha )=ABH/HX1Y1\\tan(90-\alpha )=ABH/(X1Y1X2Y2-HX1Y1)\end{cases}}\Longleftrightarrow {\begin{cases}ABH=tan(\alpha )*HX1Y1\\ABH=tan(90-\alpha )*(X1Y1X2Y2-HX1Y1)\end{cases}}\Longleftrightarrow tan(\alpha )*HX1Y1=tan(90-\alpha )*(X1Y1X2Y2-HX1Y1)\Longleftrightarrow tan(\alpha )*HX1Y1+tan(90-\alpha )*HX1Y1=tan(90-\alpha )*X1Y1X2Y2\Longleftrightarrow (tan(\alpha )+tan(90-\alpha ))*HX1Y1=tan(90-\alpha )*X1Y1X2Y2\Longleftrightarrow HX1Y1=(tan(90-\alpha )*X1Y1X2Y2)/(tan(\alpha )+tan(90-\alpha ))\Longleftrightarrow HX1Y1=X1Y1X2Y2*\cos(\alpha )^{2}

Code en Python 3

Python travaille avec les radians, donc 90 degrés = pi/2 radians

from math import sqrt, cos, sin, tan, pi
from cmath import phase
beta = phase(X2 + Y2 * 1j - (X1 + Y1 * 1j))
HX1Y1 = sqrt((Y2 - Y1)**2 + (X2 - X1)**2) * cos(alpha)**2
ABX1Y1 = HX1Y1 / cos(alpha)
A = X1 + ABX1Y1 * cos(alpha + beta)
B = Y1 + ABX1Y1 * sin(alpha + beta)
C = X1 - (B - Y1)
D = Y1 + (A - X1)
E = A - (B - Y1)
F = B + (A - X1)
G = A - (Y2 - B)
H = B + (X2 - A)
I = X2 - (Y2 - B)
J = Y2 + (X2 - A)

Voir aussi

Fractale

Liens externes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.