Arbre d'intervalles

Étant donné un ensemble n d'intervalles sur une suite de nombres, on veut construire une structure de données de telle manière qu'on puisse retrouver efficacement tous les intervalles qui chevauchent un autre intervalle ou point.

On commence par prendre la plage entière de tous les intervalles et en la divisant en deux moitiés au centre_x (en pratique, centre_x devrait choisi de manière à garder l'arbre relativement équilibré). Cela donne trois ensemble d'intervalles, ceux complètement à gauche du centre_x qu'on appellera S_gauche, ceux complètement à droite du centre_x qu'on appellera S_droite, and ceux qui chevauchent le centre_x qu'on appellera S_centre.

Les intervalles dans S_gauche et S_droite sont récursivement divisés de la même manière jusqu'à ce qu'il n'y ait plus d'intervalles.

Les intervalles dans S_centre qui chevauchent le point central sont stockés dans une structure de données séparé qui est liée au nœud dans l'arbre intervalle. Cette structure de données consiste en deux listes, une contenant l'ensemble des intervalles triés par leurs points de début, et l'autre contenant l'ensemble des intervalles triés par leurs points de fin.

Le résultat est un arbre ternaire avec chaque nœud qui stocke :

• Un point central
• Un pointeur vers un autre nœud qui contient tous les intervalles de l'extrémité gauche jusqu'au point central
• Un pointeur vers un autre nœud qui contient tous les intervalles de l'extrémité droite jusqu'au point central
• Tous les intervalles qui chevauchent le point central, triés par leurs points de début
• Tous les intervalles qui chevauchent le point central, triés par leurs points de fin

Étant donné la structure de données ci-dessus, on a des requêtes qui consistant à des zones ou des points, et on retourne toutes les zones dans l'ensemble original qui chevauchent cette entrée.

Le but est de trouver tous les intervalles dans l'arbre qui chevauchent un certain point x. L'arbre est parcouru avec un algorithme récursif similaire à ce qu'on pourrait utiliser dans un arbre binaire traditionnel, mais avec une affordance supplémentaire pour les intervalles qui chevauchent le point "central" de chaque nœud.

Pour chaque nœud de l'arbre, x est comparé à centre_x, le point central utilisé dans la construction des nœuds ci-dessus. Si x est inférieur que centre_x, l'ensemble des intervalles le plus à gauche, S_gauche, est considéré. Si x est plus grand que x_centre, l'ensemble d'intervalles le plus à droite, S_droite, est considéré.

Comme chaque nœud est traité quand on traverse l'arbre depuis la racine vers une feuille, la portée dans S_centre est traitée. Si x est inférieur que centre_x, on sait que tous les intervalles dans S_centre se terminent après x, ou il ne pourraient pas aussi chevaucher x_centre. Par conséquent, on a seulement besoin de trouver les intervalles dans S_centre qui débutent avant x. On peut consulter les listes de S_centre qui ont déjà construites. Etant donné que l'on s'intéresse uniquement aux débuts des intervalles dans ce scénario, on peut consulter la liste qui est triée par les débuts. Supposons qu'on trouve le nombre le plus grand et le plus proche de x sans le dépasser dans cette liste. Toutes les plages depuis le début de la liste par rapport au point trouvé chevauche x car elles débutent avant x et finissent après x (car nous savons qu'elles chevauchent centre_x qui est plus grand que x). Ainsi, on va simplement commencer par énumérer les intervalles dans la liste jusqu'à ce que le point de départ dépasse x.

De même, si x est plus grand que centre_x, on sait que tous les intervalles dans S_centre doivent démarre avant x, donc on trouve ces intervalles qui finissent après x en utilisant la liste triée par la fin des intervalles.

Si x correspond exactement à centre_x, tous les intervalles dans S_centre peuvent être ajoutés aux résultats sans autres traitements et le parcours de l'arbre peut être arrêté.

Pour avoir comme résultat un intervalle r qui intersecte notre intervalle de requête q un des points suivants doit s'avérer :

• le point de début et/ou de fin de r est dans q ; ou
• r renferme complètement q.

En premier on trouve tous les intervalles avec les points de début et/ou de fin dans q en utilisant un arbre construit séparément. Dans le cas unidimensionnel, on peut utiliser un arbre de recherche contenant tous les points de début et de fin de l'ensemble des intervalles, chacun avec un pointeur vers son intervalle correspondant. Une recherche binaire en un temps O(log n) pour le début et la fin de q révèle les points minimum et maximum à considérer. Chaque point avec ses plages de références (un intervalle qui chevauche q) est ajouté à la liste des résultats. Une attention doit être apportée afin d'éviter les doublons, étant donné qu'un intervalle peut à la fois être au début et à la fin de q. Cela peut être effectué un utilisant un marqueur binaire sur chaque intervalle afin de signaler s'il a déjà été ajouté à l'ensemble des résultats.

Enfin, on doit trouver les intervalles qui renferment q. Afin de les trouver, on choisit n'importe quel point à l'intérieur de q et on utilise l'algorithme ci-dessus afin de trouver tous les intervalles qui l'intersectent (de nouveau, faire attention à enlever les doublons).

La structure de données arbre intervalle peut être généralisée pour une dimension plus grande N avec des requêtes similaires; un même temps de construction et un stockage en O(n log n).

Premièrement, un arbre de portée en N dimensions est construit, ce qui permet de retrouver efficacement tous les éléments dont les points de début et de fin sont à l'intérieur de la région R de la requête. Une fois que les zones correspondantes sont trouvées, la dernière chose qui reste est les zones qui recouvrent la région dans certains dimensions. Afin de trouver ces recouvrements, n arbres intervalle sont créés, et un axe intersectant R est interrogé pour chaque. Par exemple, en deux dimensions, le bas du carré R (ou toute autre ligne horizontale intersectant R) sera interrogé contre l'arbre d'intervalle construit sur l'axe horizontal. De même, la gauche (ou tout autre ligne verticale intersectant R) sera interrogé contre l'arbre d'intervalle construit sur l'axe vertical.

Chaque arbre intervalle a aussi besoin d'une addition pour les dimensions plus grandes. Pour chaque nœud que l'on traverse dans l'arbre, x est comparé avec S_centre pour trouver les chevauchements. Au lieu de deux listes de points triés que nous avons utilisé dans le cas unidimensionnel, a arbre de portée est construit. Cela permet de retrouver efficacement tous les points dans S_centre qui chevauchent la région R.

Si après avoir supprimé un intervalle de l'arbre, le nœud contenant cet intervalle n'en contient plus, ce nœud pourrait être supprimé de l'arbre. Ceci est plus compliqué qu'une simple opération de suppression dans un arbre binaire.

Un intervalle peut chevaucher le point central de plusieurs nœuds dans l'arbre. Étant donné que chaque nœud stocke les intervalles qui le chevauchent, tous les intervalles complètement à gauche de son point central dans le sous-arbre gauche, similaire pour le sous-arbre droit, il survient que chaque intervalle est stocké dans le nœud le plus proche de la racine à partir de l'ensemble de nœuds qui ont un point central qui est chevauché.

La suppression normale dans un arbre binaire (dans le cas où le nœud supprimé a deux fils) implique de promouvoir un nœud qui était une feuille à venir à la place du nœud qui est supprimé (usuellement le fils le plus à gauche du sous-arbre droit, ou le fils le plus à droite du sous-arbre gauche).

Suppression, dans un arbre binaire de recherche, d'un nœud qui a deux fils.

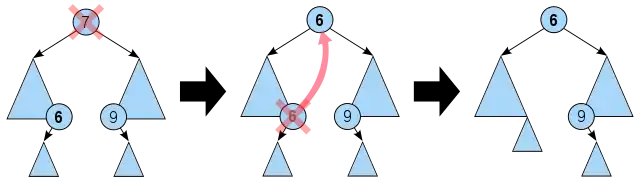
Comme résultat de cette promotion, certains nœuds qui étaient au-dessus du nœud promu vont devenir ses descendants. Il est nécessaire de chercher ces nœuds pour les intervalles qui chevauchent aussi le nœud promu, et déplacer ces intervalles dans le nœud promu. Comme conséquence, cela peut amener à de nouveaux nœuds vides, qui devront être supprimés, en suivant à nouveau le même algorithme.

Le même problème qui affecte la suppression affecte aussi les opérations de rotations. La rotation doit préserver l'invariant qui dit que chaque nœud doit être aussi proche que possible de la racine.

Des performances peuvent être gagnées si l'arbre évite des traversées inutiles. Cela peut se produire en ajoutant des intervalles qui existent déjà ou en supprimant des intervalles qui n'existent pas.

Un ordre total peut être défini sur les intervalles en les ordonnant en premier sur leurs bornes minimales et ensuite sur leurs bornes maximales. Ensuite, une vérification d'appartenant peut être effectuée en un temps O(log n), contre O(k + log n) pour trouver les doublons si k intervalles chevauchent l'intervalle qui doit être inséré ou supprimé. Cette solution a l'avantage de ne pas nécessité de structures additionnelles. Le changement est simplement algorithmique. Le désavantage est que la requête d'appartenant prend un temps O(log n).

Alternativement, au taux de O(n) mémoire, les requêtes d'appartenance peuvent être implémentées avec une table de hachage, mis à jour en même temps que l'arbre intervalle. Cela ne nécessite pas forcément le double de la mémoire requise, si les intervalles sont stockés par référence et non pas par valeur.

L'étiquette de chaque nœud est l'intervalle lui-même, par conséquent les nœuds sont triés d'abord par valeur minimale puis par valeur maximale, et la valeur de chaque nœud est l'extrémité de l'intervalle :

 public void add(Interval i) {
     put(i, i.getEnd());
 }

Pour la recherche d'un intervalle, on parcourt l'arbre, en utilisant l'étiquette (n.getKey()) et la valeur maximale (n.getValue()) pour omettre les branches qui ne peuvent pas chevaucher la requête. Le cas le plus simple est la requête d'un point :

 // Recherche de tous les intervalles contenant "p", démarrant avec le
 // nœud "n" et ajout des correspondances d'intervalles à la liste "result"
 public void search(IntervalNode n, Point p, List<Interval> result) {
     // Ne pas chercher des nœuds qui n'existent pas
     if (n == null)
         return;
 
     // Si p est à droite du point le plus à droite que n'importe quel intervalle
     // dans ce nœud et tous les fils, il n'y aura pas de correspondance
     if (p.compareTo(n.getValue()) > 0)
         return;
 
     // Recherche du fils gauche
     if (n.getLeft() != null)
         search(IntervalNode (n.getLeft()), p, result);
 
     // Vérifier ce nœud
     if (n.getKey().contains(p))
         result.add(n.getKey());
 
     // Si p est à gauche du début de cet intervalle,
     // alors il ne peut pas être dans n'importe quel fils à droite
     if (p.compareTo(n.getKey().getStart()) < 0)
         return;
 
     // Sinon, rechercher dans le fils droit
     if (n.getRight() != null)
         search(IntervalNode (n.getRight()), p, result);
 }

où

a.compareTo(b) retourne une valeur négative si a < b

a.compareTo(b) retourne zéro si a = b

a.compareTo(b) retourne une valeur positive si a > b

Le code pour chercher un intervalle est similaire, excepté pour la vérification au milieu :

 // Vérifier ce nœud 
 if (n.getKey().overlapsWith(i))
     result.add (n.getKey());

overlapsWith() est défini comme ceci :

 public boolean overlapsWith(Interval other) {
     return start.compareTo(other.getEnd()) <= 0 &&
            end.compareTo(other.getStart()) >= 0;
 }

Les arbres augmentées peuvent être étendus à de plus grandes dimensions en parcourant les dimensions à chaque niveau de l'arbre . Par exemple, pour deux dimensions, les niveaux impairs de l'arbre peuvent contenir les zones pour la coordonnée-x, pendant que les niveaux pairs contiennent les zones pour la coordonnée-y. Cette convertit effectivement la structure de données d'un arbre binaire augmenté à un arbre kd augmenté, ce qui, par conséquent, complique significativement les algorithmes d'équilibrage pour les insertions et les suppressions.

Une solution plus simple est d'utiliser des arbres intervalle imbriqués. Premièrement, créer un arbre en utilisant les zones pour la coordonnée-y. Maintenant, pour chaque nœud dans l'arbre, ajouter un autre arbre intervalle sur les zones-x, pour tous les éléments qui ont la même zone-y que celle du nœud.

L'avantage de cette solution est qu'elle peut être étendu à un nombre de dimension arbitraire en utilisant le même code de base.

Au début, le coût additionnel des arbres intervalle imbriqués peut sembler prohibitif, mais ce n'est généralement pas le cas. Comme pour la solution précédente pour les non-imbriqués, un nœud est nécessaire par coordonnée-x, amenant le même nombre de nœuds pour les deux solutions. Le seul surcoût additionnel est les structures de l'arbre imbriqué, une par intervalle vertical. Cette structure est usuellement de taille négligeable, consistant uniquement en un pointeur vers la racine du nœud, et possiblement le nombre de nœuds et la profondeur de l'arbre.

En utilisant seulement les valeurs de début et de fin de deux intervalles ${\displaystyle \left(a_{i},b_{i}\right)}$, pour ${\displaystyle i=0,1}$, le test de chevauchement peut être effectué comme ceci :

${\displaystyle a_{0}<b_{1}}$ et ${\displaystyle a_{1}>b_{0}}$

Cela peut être simplifié en utilisant la somme et la différence :

${\displaystyle s_{i}=a_{i}+b_{i}}$

${\displaystyle d_{i}=b_{i}-a_{i}}$

Ce qui réduit le test de chevauchement à :

${\displaystyle \left|s_{1}-s_{0}\right|<d_{0}+d_{1}}$

Ajouter de nouveaux intervalles dans l'arbre est pareil que pour un arbre binaire de recherche en utilisant la valeur médiane comme étiquette. On pousse ${\displaystyle d_{i}}$ dans le tas binaire associé avec le ${\displaystyle d_{i}}$, et on met à jour la valeur minimum et maximum possible associée avec tous les nœuds au-dessus.

Utilisons ${\displaystyle a_{q},b_{q},m_{q},d_{q}}$ pour la requête d'intervalle, et ${\displaystyle M_{n}}$ pour l'étiquette d'un nœud (comparé à ${\displaystyle m_{i}}$ d'intervalles).

On commence avec le nœud racine, dans chaque nœud, on vérifie en premier s'il est possible que notre requête d'intervalle se chevauche avec le nœud du sous-arbre en utilisant les valeurs minimales et maximales du nœud (si cela ne l'est pas, on ne continue pas pour ce nœud).

Ensuite on calcule ${\displaystyle \min \left\{d_{i}\right\}}$ pour les intervalles dans ce nœud (pas ses fils) qui chevauchent avec l'intervalle de la requête (en sachant ${\displaystyle m_{i}=M_{n}}$) :

${\displaystyle \min \left\{d_{i}\right\}=\left|m_{q}-M_{n}\right|-d_{q}}$

et on effectue une requête sur son tas binaire pour le ${\displaystyle d_{i}}$ plus grand que ${\displaystyle \min \left\{d_{i}\right\}}$.

Ensuite on passe à travers les files gauche et droite du nœud, en faisant la même chose. Dans le pire des cas, nous devons scanner tous les nœuds de l'arbre binaire de recherche, mais étant donné que la requête sur un tas binaire est optimale, ceci est acceptable (un problème à 2 dimensions ne peut pas être optimal dans les deux dimensions).

Cet algorithme est attendu pour être plus rapide qu'un traditionnel arbre intervalle (arbre augmenté) pour les opérations de recherche. Ajouter un élément est un peu plus lent en pratique, car l'ordre de croissance est le même.