Angles alternes-internes

Deux angles formés par deux droites coupées par une sécante sont dits alternes-internes si :

1. ils sont situés de part et d'autre de la sécante ;
2. ils sont situés entre les deux droites ;
3. ils ne sont pas adjacents.

Angles alternes-internes avec deux droites quelconques.

Les droites ${\displaystyle (xx')}$ et ${\displaystyle (yy')}$ sont coupées respectivement en ${\displaystyle A}$ et en ${\displaystyle B}$ par la sécante ${\displaystyle (tt')}$.

${\displaystyle {\widehat {xAB}}}$ et ${\displaystyle {\widehat {ABy'}}}$ sont des angles alternes-internes.

Propriété

• Si deux droites parallèles sont coupées par une sécante, alors elles forment des angles alternes-internes de même mesure.
• Réciproquement, si deux droites coupées par une sécante forment des angles alternes-internes de même mesure, alors ces deux droites sont parallèles.

Exemple

Sur la figure suivante, les droites a et b sont parallèles, s est une sécante quelconque.

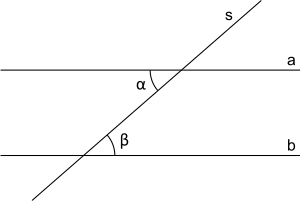${\displaystyle \alpha }$ et ${\displaystyle \beta }$ sont des angles alternes-internes égaux .

Angles alternes-externes