Algorithme de Bernstein-Vazirani

Soit un oracle qui implémente une fonction ${\displaystyle f\colon \{0,1\}^{n}\rightarrow \{0,1\}}$ dans laquelle ${\displaystyle f(x)}$ est un produit scalaire entre ${\displaystyle x}$ et une chaîne secrète ${\displaystyle s\in \{0,1\}^{n}}$ modulo 2, ${\displaystyle f(x)=x\cdot s=x_{1}s_{1}\oplus x_{2}s_{2}\oplus \cdots \oplus x_{n}s_{n}}$. Quelle est la valeur de ${\displaystyle s}$ ?

En informatique "classique", la méthode la plus efficace pour retrouver la chaîne secrète consiste à évaluer la fonction ${\displaystyle n}$ fois avec comme valeurs d'entrée ${\displaystyle x=2^{i}}$ pour tout ${\displaystyle i\in \{0,1,...,n-1\}}$[2] :

${\displaystyle {\begin{aligned}f(1000\cdots 0_{n})&=s_{1}\\f(0100\cdots 0_{n})&=s_{2}\\f(0010\cdots 0_{n})&=s_{3}\\&\,\,\,\vdots \\f(0000\cdots 1_{n})&=s_{n}\\\end{aligned}}}$

Avec un calculateur quantique, une seule requête sera suffisante[2] :

Appliquer une transformée de Hadamard aux ${\displaystyle n}$ qubits ${\displaystyle |0\rangle ^{\otimes n}}$ pour obtenir :

${\displaystyle {\frac {1}{\sqrt {2^{n}}}}\sum _{x=0}^{2^{n}-1}|x\rangle .}$

Ensuite, appliquer l'oracle ${\displaystyle U_{f}}$ qui transforme ${\displaystyle |x\rangle \to (-1)^{f(x)}|x\rangle }$. Cela peut être simulé au moyen de l'oracle standard qui transforme ${\displaystyle |b\rangle |x\rangle \to |b\oplus f(x)\rangle |x\rangle }$ en appliquant l'oracle à ${\displaystyle {\frac {|0\rangle -|1\rangle }{\sqrt {2}}}|x\rangle }$ (${\displaystyle \oplus }$ représente une addition modulo 2).

Cela transforme la superposition en :

${\displaystyle {\frac {1}{\sqrt {2^{n}}}}\sum _{x=0}^{2^{n}-1}(-1)^{f(x)}|x\rangle .}$

Une nouvelle transformée de Hadamard est appliquée à chaque qubit, de telle sorte que :

• pour les qubits où ${\displaystyle s_{i}=1}$, l'état est converti de ${\displaystyle |-\rangle }$ à ${\displaystyle |1\rangle }$
• pour les qubits où ${\displaystyle s_{i}=0}$, l'état est converti de ${\displaystyle |+\rangle }$ à ${\displaystyle |0\rangle }$

Pour obtenir ${\displaystyle s}$, une mesure selon la base standard (${\displaystyle \{|0\rangle ,|1\rangle \}}$) est effectuée sur les qubits.

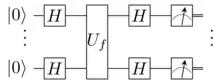
L'algorithme peut donc être représenté ainsi, où ${\displaystyle H^{\otimes n}}$ représente la transformée de Hadamard sur ${\displaystyle n}$ qubits :

${\displaystyle |0\rangle ^{n}\xrightarrow {H^{\otimes n}} {\frac {1}{\sqrt {2^{n}}}}\sum _{x\in \{0,1\}^{n}}|x\rangle \xrightarrow {U_{f}} {\frac {1}{\sqrt {2^{n}}}}\sum _{x\in \{0,1\}^{n}}(-1)^{f(x)}|x\rangle \xrightarrow {H^{\otimes n}} {\frac {1}{2^{n}}}\sum _{x,y\in \{0,1\}^{n}}(-1)^{f(x)+x\cdot y}|y\rangle =|s\rangle }$

La raison pour laquelle l'état final est ${\displaystyle |s\rangle }$ est que, pour un ${\displaystyle y}$ donné :

${\displaystyle {\frac {1}{2^{n}}}\sum _{x\in \{0,1\}^{n}}(-1)^{f(x)+x\cdot y}={\frac {1}{2^{n}}}\sum _{x\in \{0,1\}^{n}}(-1)^{x\cdot s+x\cdot y}={\frac {1}{2^{n}}}\sum _{x\in \{0,1\}^{n}}(-1)^{x\cdot (s\oplus y)}=1{\text{ si }}s\oplus y={\vec {0}},\,0{\text{ sinon}}.}$

Puisque ${\displaystyle s\oplus y={\vec {0}}}$ est vrai seulement quand ${\displaystyle s=y}$, cela signifie que la seule amplitude non nulle correspond à ${\displaystyle |s\rangle }$.

(en) Cet article est partiellement ou en totalité issu de la page de Wikipédia en anglais intitulée « Bernstein–Vazirani algorithm » (voir la liste des auteurs).