2-opt

Exemple de permutation

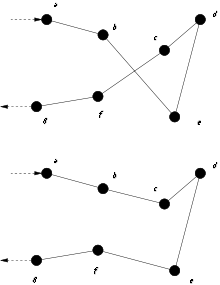
2-opt est un algorithme itératif : à chaque étape, on supprime deux arêtes de la solution courante et on reconnecte les deux tours ainsi formés. Cette méthode permet, entre autres, d'améliorer le coût des solutions en supprimant les arêtes sécantes lorsque l'inégalité triangulaire est respectée (voir figure ci-contre). Sur le schéma de droite, la route <a; b; e; d; c; f; g> est changée en <a; b; c; d; e; f; g> en inversant l'ordre de visite des villes e et c. Plus généralement, lorsqu'on inverse l'ordre de parcours de deux villes, il faut aussi inverser l'ordre de parcours de toutes les villes entre ces deux villes.

On peut donner une description plus formelle de l’heuristique. Soit un graphe ${\displaystyle G=(V,E)}$ et ${\displaystyle H}$ un cycle hamiltonien dans ${\displaystyle G}$ muni d’une fonction coût renvoyant la somme des poids des arêtes composant le cycle.

Dans le cas du problème du voyageur de commerce géométrique, i.e. quand l'inégalité triangulaire des poids est respectée[2], la permutation consiste généralement à remplacer les arêtes par leurs diagonales (cf. le schéma ci-contre).

L’algorithme s’énonce alors ainsi[3] :

• trouver une 2-permutation de ${\displaystyle H}$ produisant le cycle ${\displaystyle H'}$ tel que coût(H') < coût(H) ;
• remplacer ${\displaystyle H}$ par ${\displaystyle H'}$ ;
• recommencer tant qu’une telle 2-permutation est possible.

Pour des raisons de performance, la solution initiale H est souvent générée par une heuristique constructiviste ou gloutonne rapide, voire aléatoirement. On peut noter que diverses stratégies peuvent être appliquées lors du choix de la permutation : ce peut être la première trouvée, la meilleure ou la pire au regard de la tournée courante, ou encore un choix aléatoire parmi un ensemble de permutations admissibles.

Voici une transcription directe appliquée au cas du voyageur de commerce géométrique :

Une permutation n’est admissible que si elle réduit strictement le coût total du cycle hamiltonien. En particulier, cela implique que chaque cycle hamiltonien est visité au plus une fois, garantissant la terminaison de l’algorithme en au plus ${\displaystyle n!}$ permutations. Il existe des instances où 2-opt prend un temps exponentiel, même dans le cas euclidien[4]. En pratique cependant, on observe que l’heuristique se comporte en ${\displaystyle O(n^{2})}$[5]. Pour des problèmes euclidiens avec des villes uniformément distribuées dans le carré unité et en utilisant une structure de données permettant d'effectuer une modification 2-opt en ${\displaystyle O(1)}$, Taillard[6] a observé une complexité très légèrement supérieure à ${\displaystyle O(n^{2})}$. Diverses méthodes permettent d’optimiser ce résultat en calculant par exemple au préalable une liste des m sommets les plus proches de chaque ville (donc m ≤ n) ; une complexité de ${\displaystyle O(mn)}$ peut ainsi être obtenue[7].

Communément, on mesure l’efficacité des différentes heuristiques du voyageur de commerce en comparant la distance de la solution obtenue avec une borne inférieure de la solution optimale (par exemple, la borne de Held-Karp). Ce faisant, diverses études empiriques tendent à montrer que l’algorithme 2-opt donne de bons résultats par rapport aux heuristiques constructivistes, avec un écart par rapport à la borne allant de 4 à 7 % environ – c’est-à-dire au pire entre 4 et 7 % de la solution optimale[8].

La principale limite de 2-opt réside dans le fait qu’il ne fournit pas de garantie satisfaisante quant à la qualité de la solution finale : l’algorithme est sujet à tomber dans des minima locaux assez rapidement. On note aussi que la nature de la solution initiale peut influer grandement sur les résultats[8].

• Algorithme de Lin-Kernighan
• Recherche locale
• Problème du voyageur de commerce
• Problème de tournées de véhicules
• Algorithme de Christofides, un algorithme d'approximation pour le cas métrique du voyageur de commerce

• Implantation pratique dans le cadre de la coupe de france de robotique 2004
• Exemple interactif via une applet