Équation de Monod

Vitesse de croissance des micro-organismes considérés en fonction de la concentration en substrat S limitant cette croissance.

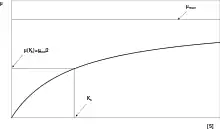
L'équation de Monod décrit la vitesse de croissance μ de micro-organismes donnés en fonction de la concentration en substrat [S] limitant cette croissance de la façon suivante[2] :

${\displaystyle \mu =\mu _{max}{\frac {[S]}{K_{S}+[S]}}}$

où :

• μ est la vitesse de croissance des micro-organismes considérés;
• μ_max est la vitesse de croissance maximale de ces micro-organismes;
• [S] est la concentration du substrat S limitant la croissance des micro-organismes considérés (carence, pénurie, en substrat limitant, p. ex. le phosphate indispensable à la synthèse de l'ATP);
• K_s est la constante de demi-vitesse c'est-à-dire la valeur de [S] quand μ/μ_max vaut 0,5.

Les coefficients μ_max et K_s sont de nature empirique (expérimentale): leurs valeurs sont spécifiques et conditionnelles. En effet, ces valeurs diffèrent selon les espèces de micro-organismes considérés et dépendent également des conditions expérimentales ou ambiantes comme p. ex. de la température, du pH de la solution, des conditions redox du milieu (aérobie, anaérobie) et de la composition du milieu nutritif utilisé pour la mise en culture des micro-organismes.

• Boues activées
• Équation de Michaelis-Menten