Équation de Cahn-Hilliard

Les mathématiciens s'intéressent à l'existence d'une solution unique à l'équation de Cahn-Hilliard, donnée par des données initiales lisses. La preuve s'appuie essentiellement sur l'existence d'une fonctionnelle de Liapunov. Plus spécifiquement, si l'on identifie

$${\displaystyle F[c]=\int d^{n}x\left[{\frac {1}{4}}\left(c^{2}-1\right)^{2}+{\frac {\gamma }{2}}\left|\nabla c\right|^{2}\right],}$$

à une fonctionnelle d'énergie libre, alors

$${\displaystyle {\frac {dF}{dt}}=-\int d^{n}x\left|\nabla \mu \right|^{2},}$$

de sorte que l'énergie libre décroît avec le temps. Ceci indique aussi que la séparation en domaines est la finalité asymptotique de cette équation.

Dans des expériences réelles, la séparation en domaines d'un fluide binaire initialement mélangé est observée. La séparation est caractérisée par les faits suivants.

Évolution de données initiales aléatoires avec l'équation de Cahn-Hilliard avec ${\displaystyle \gamma =0.5}$ et ${\displaystyle C=0}$, démontrant la séparation des phases.

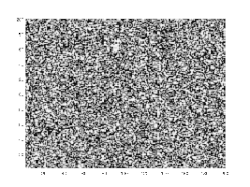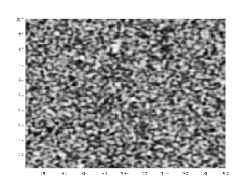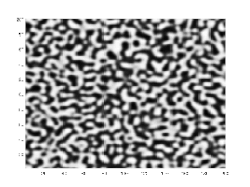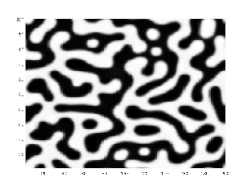
• Il y a une couche de transition entre les domaines séparés, avec un profile donné par la fonction ${\displaystyle c(x)=\tanh \left({\frac {x}{\sqrt {2\gamma }}}\right)}$, d'où une largeur typique de ${\displaystyle {\sqrt {\gamma }}}$ car cette fonction est une solution à l'équilibre de l'équation de Cahn-Hilliard.
• Les domaines grandissent avec le temps selon une loi de puissance. Si ${\displaystyle L(t)}$ est une taille de domaine typique, alors ${\displaystyle L(t)\propto t^{1/3}}$. C'est la loi de Lifshitz-Slyozov, qui a été prouvée rigoureusement pour l'équation de Cahn-Hilliard et observée dans des simulations numériques et des expériences réelles avec des fluides binaires.
• L'équation de Cahn-Hilliard a une forme de loi de conservation, ${\displaystyle {\frac {\partial c}{\partial t}}=\nabla \cdot \mathbf {j} (x)}$, avec ${\displaystyle \mathbf {j} (x)=D\nabla \mu }$. Ainsi le processus de séparation de phase conserve la concentration totale ${\displaystyle C=\int d^{n}xc\left(x,t\right)}$, de sorte que ${\displaystyle {\frac {dC}{dt}}=0}$.
• Lorsqu'une phase est significativement plus abondante, l'équation de Cahn-Hilliard peut montrer le phénomène connu sous le nom de mûrissement d'Ostwald, où la phase minoritaire forme des gouttelettes sphériques, et les gouttelettes les plus petites sont absorbées par diffusion dans les plus grandes.

Les équations de Cahn-Hilliard trouvent des applications dans des domaines divers, des fluides complexes à la matière souple (écoulement de fluide à l'interface, science des polymères et applications industrielles). La solution de l'équation de Cahn-Hilliard pour un mélange binaire coïncide bien avec la solution d'un problème de Stefan et le modèle de Thomas et Windle[1]. Les chercheurs s'intéressent actuellement au couplage de la séparation de phase de l'équation de Cahn-Hilliard aux équations de Navier-Stokes pour les écoulements de fluide.

• Décomposition spinodale
• Équation d'Allen-Cahn

• Cahn et Hilliard, « Free Energy of a Nonuniform System. I. Interfacial Free Energy », The Journal of Chemical Physics, AIP Publishing, vol. 28, n^o 2,‎ 1958, p. 258–267 (ISSN 0021-9606, DOI 10.1063/1.1744102)
• Bray, « Theory of phase-ordering kinetics », Advances in Physics, Informa UK Limited, vol. 43, n^o 3,‎ 1994, p. 357–459 (ISSN 0001-8732, DOI 10.1080/00018739400101505, arXiv cond-mat/9501089)
• Zhu, Chen, Shen et Tikare, « Coarsening kinetics from a variable-mobility Cahn-Hilliard equation: Application of a semi-implicit Fourier spectral method », Physical Review E, American Physical Society (APS), vol. 60, n^o 4,‎ 1^er octobre 1999, p. 3564–3572 (ISSN 1063-651X, DOI 10.1103/physreve.60.3564)
• Elliott et Songmu, « On the Cahn-Hilliard equation », Archive for Rational Mechanics and Analysis, Springer Nature, vol. 96, n^o 4,‎ 1986, p. 339–357 (ISSN 0003-9527, DOI 10.1007/bf00251803)
• Areias, Samaniego et Rabczuk, « A staggered approach for the coupling of Cahn–Hilliard type diffusion and finite strain elasticity », Computational Mechanics, Springer Science and Business Media LLC, vol. 57, n^o 2,‎ 17 décembre 2015, p. 339–351 (ISSN 0178-7675, DOI 10.1007/s00466-015-1235-1)
• Hashimoto, Matsuzaka, Moses et Onuki, « String Phase in Phase-Separating Fluids under Shear Flow », Physical Review Letters, American Physical Society (APS), vol. 74, n^o 1,‎ 2 janvier 1995, p. 126–129 (ISSN 0031-9007, DOI 10.1103/physrevlett.74.126)
• T. Ursell, “Cahn–Hilliard Kinetics and Spinodal Decomposition in a Diffuse System,” California Institute of Technology (2007).