Triangulation de Pitteway

En géométrie algorithmique, une triangulation de Pitteway est une triangulation d'un ensemble de points dans laquelle le plus proche voisin de n'importe quel point p à l'intérieur de la triangulation est l'un des sommets du triangle contenant p.

À gauche: Une triangulation de Pitteway. Chaque arête de la triangulation de Delaunay, en noir, coupe son dual associé dans le diagramme de Voronoi, en pointillé bleu. À droite : une triangulation de Delaunay qui n'est pas une triangulation de Pitteway : l'arête rouge de la triangulation de Delaunay ne coupe pas son dual, en rouge pointillé, dans le diagramme de Voronoi. Certains points à l'intérieur du triangle supérieur sont plus proches du sommet du bas que des trois autres.

Histoire

Le concept a été introduit par Michael Pitteway en 1973[1]. McLain en parle aussi en 1976[2] Le nom "triangulation de Pitteway" date de Okabe et al., en 2000[3].

Ensemble de points sans triangulation de Pitteway

Le point A, en cyan, est plus proche du sommet B, en vert, que des autres sommets, en bleu.

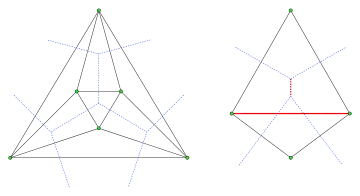
Gold, en 1978[4], fait remarquer que tous les ensembles de points n'admettent pas forcément de triangulation de Pitteway. Par exemple, n'importe quelle triangulation d'un pentagone régulier possède un triangle isocèle tel qu'un point p proche de milieu d'un des côtés du triangle isocèle sera plus proche d'un sommet en dehors du triangle que des sommets du triangle.

Relation avec d'autres graphes géométriques

Quand une triangulation de Pitteway existe, le milieu de chaque arête à l'intérieur de la triangulation doit avoir comme plus proches voisins les deux sommets de l'arête, car autrement la propriété de Pitteway serait violée pour les points proches de ce milieu dans l'un des deux triangles adjacents. Ainsi, un cercle ayant pour diamètre cette arête ne doit pas contenir de sommet, ce qui fait que la triangulation de Pitteway correspond au graphe Gabriel augmenté de l'enveloppe convexe de l'ensemble de points. Réciproquement, quand un graphe Gabriel et une enveloppe convexe forment une triangulation, c'est une triangulation de Pitteway.

Comme le graphe Gabriel et l'enveloppe convexe sont des parties de la triangulation de Delaunay, cela signifie qu'une triangulation de Pitteway, lorsqu'elle existe, est unique pour un ensemble de points en position général et coïncide avec la triangulation de Delaunay.

Dans une triangulation de Pitteway, chaque arête pq soit appartient à l'enveloppe convexe, soit coupe l'une des arêtes du diagramme de Voronoi séparant les cellules contenant les points p et q, c'est-à-dire le dual à la triangulation. Pour certaines sources, cette propriété est utilisée pour définir une triangulation de Pitteway comme une triangulation de Delaunay dans laquelle toutes les arêtes internes coupent leur arête duale dans le diagramme de Voronoi. Les arêtes externes peuvent ne pas couper leurs duales[3].

Voir aussi

Références

M. L. V. Pitteway, "Computer graphics research in an academic environment", Datafair '73, 1973
(en) D. H. McLain, « Two dimensional interpolation from random data. », The Computer Journal, vol. 19, n^o 2,‎ mai 1976, p. 178–181 (DOI 10.1093/comjnl/19.2.178)
Okabe, Atsuyuki; Boots, Barry N.; Chiu, Sung Nok; Sugihara, Kokichi (2000), Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, Wiley .
Gold, C. M. (1978), "practical generation and use of geographic triangular element data structures", in Dutton, G., Proceedings First International Advanced Study Symposium on Topological Data Structures for Geographic Information Systems. Harvard Papers on Geographic Information Systems, vol. 5 — Data Structures: Surficial and Multi Dimensional., Boston: Laboratory for Computer Graphics and Spatial Analysis, Harvard University, pp. 1–18 .

Dobrin, Adam (2005), Review of Properties and Variations of Voronoi Diagrams, Whitman College

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.