Transmission acoustique

Une onde incidente, de type longitudinale ou transversale, peut générer, après traversée d’une interface séparant deux milieux denses suivant l'angle d'incidence, soit deux ondes propagatives (une onde longitudinale et une onde transversale) soit une seule onde propagative (transversale ou longitudinale). Lorsque le type de l’onde transmise n’est pas identique à celui de l’onde incidente, il y a conversion de mode.

Dans le cas général de l’incidence oblique d’une onde plane, à une interface plane entre deux solides élastiques isotropes, il y a réflexion et transmission de l’onde avec conversion de mode. Il y a donc génération de quatre ondes différentes correspondant aux deux modes possibles dans chaque solide.

[1]Directions de propagation à une interface

[2]

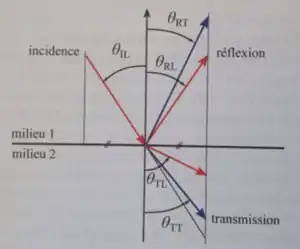
Dans le cas général (comme illustré dans la figure ci-contre), cette loi peut s’écrire avec des nombres complexes en définissant pour :

${\displaystyle {\sin(\theta _{IL}) \over C_{L1}}={\sin(\theta _{RL}) \over C_{L1}}={\sin(\theta _{RT}) \over C_{T1}}={\sin(\theta _{TL}) \over C_{L2}}={\sin(\theta _{TT}) \over C_{T2}}}$

Dans le cas de l’incidence normale d’une onde longitudinale plane à une interface, la loi de Snell-Descartes montre que l’onde longitudinale réfléchie et celle transmise sont aussi normales à l’interface.

En utilisant le modèle de ligne de transmission, les équations qui régissent le phénomène peuvent être facilement obtenues en tenant compte de la continuité des composantes de contraintes et des vitesses des particules à l'interface. Deux contraintes[3] sont pertinentes pour les conditions aux limites:

${\displaystyle \tau _{yy}=\lambda {du_{z} \over dz}+(\lambda +2\mu ){du_{y} \over dy}}$

${\displaystyle \tau _{zy}=\mu ({du_{y} \over dz}+{du_{z} \over dy})}$

Tels que: ${\displaystyle \mu _{1}=\rho _{1}c_{S1}^{2}}$ , ${\displaystyle \lambda _{1}+2\mu _{1}=\rho _{1}c_{d1}^{2}}$ , ${\displaystyle \mu _{2}=\rho _{2}c_{S2}^{2}}$ , ${\displaystyle \lambda _{2}+2\mu _{2}=\rho _{2}c_{d2}^{2}}$.

La continuité du mouvement et l’équilibre des contraintes s’écrivent sous forme matricielle[3] :

${\displaystyle {\begin{vmatrix}{sin\theta _{P1} \over \rho _{1}c_{P1}}&{sin\theta _{S1} \over \rho _{1}c_{S1}}&{-sin\theta _{P2} \over \rho _{2}c_{P2}}&{sin\theta _{S2} \over \rho _{2}c_{S2}}\\{cos\theta _{P1} \over \rho _{1}c_{P1}}&{-sin\theta _{S1} \over \rho _{1}c_{S1}}&{cos\theta _{P2} \over \rho _{2}c_{P2}}&{sin\theta _{S2} \over \rho _{2}c_{S2}}\\-cos(2\theta _{S1})&sin(2\theta _{S1})&cos(2\theta _{S2})&cos(2\theta _{S2})\\{sin(2\theta _{P1}) \over c_{P1}^{2}c_{S1}^{2}}&cos(2\theta _{S1})&{sin(2\theta _{P2}) \over c_{P2}^{2}c_{S2}^{2}}&-cos(2\theta _{S2})\end{vmatrix}}}$ ${\displaystyle {\begin{vmatrix}R_{P}\\R_{S}\\T_{P}\\T_{S}\end{vmatrix}}}$ = ${\displaystyle {\begin{vmatrix}{sin\theta _{P1} \over \rho _{1}c_{P1}}\\{cos\theta _{P1} \over \rho _{1}c_{P1}}\\cos(2\theta _{S1})\\{sin(2\theta _{P1}) \over c_{P1}^{2}/c_{S1}^{2}}\end{vmatrix}}}$

Avec:

${\displaystyle \theta _{P1}}$:Angle d'incidence et de réflexion de l'onde longitudinale.

${\displaystyle \theta _{P2}}$:Angle de transmission de l'onde longitudinale.

${\displaystyle \theta _{S1}}$:Angle de réflexion de l'onde transverse.

${\displaystyle \theta _{S1}}$:Angle de transmission de l'onde transverse.

${\displaystyle c_{P1}}$, ${\displaystyle c_{P2}}$, ${\displaystyle c_{S1}}$et ${\displaystyle c_{S2}}$ sont les vitesses de phase des ondes longitudinales et transverses dans les deux milieux.

Les coefficients de réflexion et de transmission peuvent être déterminés comme suit[3]:

${\displaystyle R_{P}^{Pot}=-R_{P}R_{P}^{*},R_{S}^{Pot}=-R_{S}R_{S}^{*}{real(1/Z_{S1}^{*}) \over real(1/Z_{P1}^{*})},T_{P}^{Pot}=-T_{P}T_{P}^{*}{real(1/Z_{P2}^{*}) \over real(1/Z_{P1}^{*})},T_{S}^{Pot}=-T_{S}T_{S}^{*}{real(1/Z_{S2}^{*}) \over real(1/Z_{P1}^{*})}}$

Où l'indice « * » représente la valeur conjuguée des variables complexes et « real () » représente la composante réelle de l'impédance décrite dans les expressions suivantes[3]:

${\displaystyle Z_{P1}={c_{P1}\rho _{1} \over cos(\theta _{P1})},Z_{P2}={c_{P2}\rho _{2} \over cos(\theta _{P2})},Z_{S1}={c_{S1}\rho _{1} \over cos(\theta _{S1})},Z_{S2}={c_{S2}\rho _{2} \over cos(\theta _{S2})}}$

Exemple d'étude: Interface plexiglas-aluminium en incidence oblique

Coefficient de transmission et de réflexion en énergie pour une interface plexiglas-aluminium

Ces ondes sont souvent générées par un transducteur piézoélectrique qui transforme une impulsion électrique en vibration. En couplant (liquide) le traducteur à la pièce, et dans des conditions idéales, les ultrasons se propagent en ligne droite, à vitesse constante, jusqu’à ce qu’ils rencontrent une interface entre deux milieux. L’énergie de l’onde est alors partiellement réfléchie et transmise par cette interface macroscopique (surface de pièce, fissure, inclusion, porosité…) ou microscopique (microstructure, joint de grains…). Le traducteur de réception, permet, via un appareillage, de visualiser des échos caractéristiques des propagations ultrasonores. On mesure les amplitudes réfléchies et transmises, en fonction de la surface réfléchissante du réflecteur (donc de la taille), et le temps de vol permet de connaitre la distance à laquelle se trouve ce réflecteur.

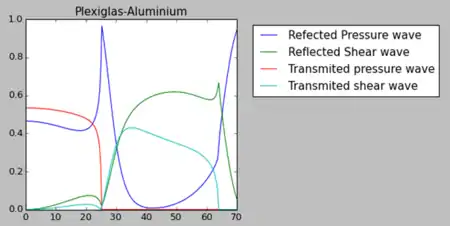
Dans le cas d’une incidence oblique, les valeurs des coefficients de transmission et de réflexion, en amplitude ou en énergie, sont plus complexes. La figure ci-contre montre les coefficients de réflexion et transmission en énergie pour une interface aluminium-plexiglas.

On retrouve bien la même valeur en énergie pour l’incidence normale (${\displaystyle E_{RL}}$=0.46 et ${\displaystyle E_{TL}}$=0.54).

Le premier angle critique (disparition de l’onde longitudinale réfractée) apparaît à 26° dans les deux cas, et le second angle critique à 61° pour le premier modèle et à 64° pour le deuxième.

On retrouve que l’amplitude la plus élevée, transmise dans l’aluminium, est pour l’onde transmise transversale obtenue avec une incidence de 32°.

[4]Onde longitudinale arrivant sur une interface fluide (non visqueux)-solide

Il existe deux angles critiques pour ce cas : le premier angle critique correspond à la disparition en surface de l’onde longitudinale transmise, soit un angle ${\displaystyle \theta _{L}^{c}}$=${\displaystyle \arcsin({c_{L1} \over c_{L2}})}$ . Le second angle critique est pour la disparition en surface de l’onde transversale transmise, soit un angle ${\displaystyle \theta _{T}^{c}}$=${\displaystyle \arcsin({c_{L1} \over c_{T2}})}$. Lorsque l’angle d’incidence est inférieur à l’angle ${\displaystyle \theta _{L}^{c}}$ , l’onde longitudinale transmise dans le solide est propagative et lorsque l’angle d’incidence est supérieur à l’angle ${\displaystyle \theta _{L}^{c}}$, elle est évanescente. De même, lorsque l’angle d’incidence est inférieur à l’angle ${\displaystyle \theta _{T}^{c}}$, l’onde transverse transmise dans le solide est propagative et lorsque l’angle d’incidence est supérieur à l’angle, elle est évanescente.

Le cas général d’une interface solide-solide peut être particularisé pour une interface liquide-solide sans avoir recours à aucune modification si le liquide est de très faible viscosité. Ce cas de figure est illustré dans la figure ci-contre, où sont tracées les évolutions des coefficients de réflexion et de transmission en énergie, en prenant comme liquide l’eau avec une viscosité égale à 10⁻¹⁰ Pa s.

Coefficient de transmission et de réflexion en énergie pour une interface eau-aluminium

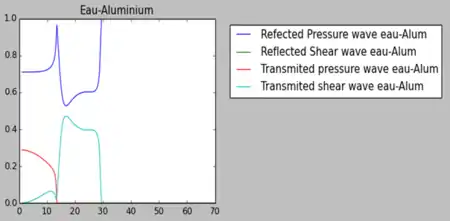
On retrouve bien les mêmes résultats en incidence normale aussi bien en incidence oblique.