Théorie JKR

La théorie JKR, des noms de Johnson, Kendall et Roberts, auteurs de l'article correspondant en 1971[1], est une théorie portant sur le phénomène d'adhésion en physique. Leur calcul[2] s'applique au contact entre une sphère et un plan, comme les calculs de Hertz ou de Derjaguin, Muller et Toporov (DMT) qui s'appliquent dans des conditions expérimentales différentes. Dans les limites de JKR, la sphère et/ou le plan est déformable, avec une réponse élastique, et il y a une interaction énergétique entre les deux surfaces (gain d'une énergie $W$ par unité de surface, appelée énergie de Dupré, lors de la mise en contact).

Test JKR avec une bille rigide sur un matériau élastique plan : cycle complet

Test JKR

Test JKR avec une bille rigide sur un matériau élastique plan : force en fonction du rayon de contact, et illustrations

Un test d'adhésion qui est aujourd'hui couramment utilisé résulte de ce calcul célèbre. Le principe est de fabriquer une sphère (molle) à partir d'un matériau adhésif à tester. Cette sphère est ensuite appuyée sur un substrat et l'on mesure l'aire de contact en fonction de la force $F$ appliquée à la sphère. Le premier avantage de ce test est que l'on peut tester de nombreux matériaux et en particulier des polymères. En effet, il est très facile de fabriquer une calotte sphérique parfaite en polymérisant une goutte de polymère fondu. De plus, l'expérience nécessite une très petite quantité de matériau.

Déroulement (description qualitative)

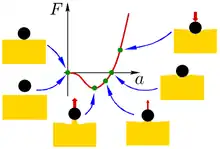
L'illustration animée présente un cycle complet d'un test JKR entre une sphère rigide et un plan élastique : approche, contact ponctuel et saut vers un contact de taille fini à force nulle, compression, décompression, traction et diminution de la taille du contact, détachement.

Test JKR avec une bille rigide et un matériau plan élastique : situation à force nulle, avec une région de contact de taille finie

Lors du premier contact, initialement ponctuel, le matériau élastique se déforme en bordure du point de contact afin d'élargir la zone de contact, ce qui permet d'abaisser l'énergie du système (énergie de Dupré $W$ par unité de surface). Ce faisant, le matériau augmente son énergie élastique. Un équilibre s'établit de manière à minimiser l'énergie. Si la bille n'est pas maintenue (force extérieure nulle), la région de contact s'établit donc à une certaine taille, non nulle. Corrélativement, la bille s'est légèrement enfoncée dans le matériau élastique. Sur la courbe, cette situation correspond au point situé sur l'axe horizontal ( $F=0$ ) à une valeur finie du rayon de contact $a$ .

Lors de la compression, en augmentant la force appliquée ( $F>0$ ), la région de contact s'élargit progressivement (points situés au-dessus de l'axe horizontal de la courbe). Lors de la décompression, on repasse par les mêmes états jusqu'au point de force nulle.

Si l'on continue, on commence à tirer ( $F<0$ ). Corrélativement, la taille de la zone de contact diminue (ce sont les points situés sous l'axe horizontal de la courbe).

Pour une certaine valeur de la force de traction, la situation devient instable : la zone de contact rétrécit brusquement et la bille se détache totalement du matériau élastique.

Estimation de l'énergie (en loi d'échelle)

La suite de l'article consiste à retrouver la formule JKR présentée ci-dessus.

Soit une sphère déformable de rayon $R$ en contact avec un demi espace rigide. Sous l'effet conjugué de la force extérieure $F$ et de l'énergie de Dupré $W$ qui favorise le contact, la bille subit un enfoncement $\delta$ . L'aire de contact avec la surface plane est un disque de rayon $a$ (on suppose $a\ll R$ ).

Énergie élastique stockée

L'ordre de grandeur de l'énergie élastique due à la déformation est celle d'un contact de Hertz :

$E_{el}\simeq E\,{\frac {a^{5}}{R^{2}}}\simeq E\,R^{1/2}\,\delta ^{5/2}$

Énergie de surface

La surface de contact apparue lors de l'approche de la sphère et du plan rapporte de l'énergie proportionnellement à l'énergie de Dupré $W$ .

L'énergie de surface totale s'écrit donc :

$E_{s}=-\pi a^{2}\,W$

Le travail effectué est de l'ordre de $E_{totale}=F\delta$

$E_{totale}=E{\frac {a^{5}}{R^{2}}}-\pi a^{2}\,W$

Comportement dans deux cas simples

L'estimation de l'énergie fournie ci-dessus permet de décrire deux cas particuliers. Une description correcte des autres situations (voir la formule complète plus bas) requiert un calcul complet.

Énergie de surface négligeable

L'énergie élastique est prépondérante sur l'énergie de surface on retombe donc sur la loi de Hertz :

Si ( $W=0$ ) on obtient alors $\delta =\left({\frac {F^{2}}{E^{2}R}}\right)^{1/3}$ .

Force extérieure négligeable

Dans le cas où les forces extérieures sont négligées, seules les forces de surface agissent sur la sphère, on minimise $E{\frac {a^{5}}{R^{2}}}-\pi a^{2}\,W$ , ce qui donne :

$a=\left({\frac {R^{2}W}{E}}\right)^{1/3}$

En tenant compte de la géométrie : $\delta =\left({\frac {W^{2}R}{E^{2}}}\right)^{1/3}$ .

Résultat JKR exact

Un calcul complet, non présenté ici, permet d'obtenir la formule complète de JKR. On constate qu'elle ne résulte pas de la simple somme des contributions de l'énergie élastique et de l'énergie de surface calculées plus haut :

$F={\frac {4\,a^{3}\,E^{\star }}{3\,R}}-{\sqrt {8\pi \,E^{\star }\,W\,a^{3}}}$ .

Notations

Ici, $F$ est la force appliquée à la sphère, $R$ son rayon, $W$ l'énergie de Dupré du problème, $a$ le rayon de la zone de contact et $E^{\star }$ une combinaison du module élastique d'Young $E$ de la sphère et de son module de Poisson $\nu$ : $E^{\star }={\frac {E}{1-\nu ^{2}}}$ . Plus précisément, si les deux matériaux sont déformables, la quantité pertinente dépend des deux modules d'Young et des deux coefficients de Poisson : ${\frac {1}{E^{\star }}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}$ .

Matériau incompressible

Dans le cas d'un matériau incompressible ( $\nu ={\frac {1}{2}}$ donc $E^{\star }={\frac {4}{3}}E$ ), le résultat JKR devient : $F={\frac {a^{3}E}{R}}-{\sqrt {6\pi \,E\,W\,a^{3}}}$ .

Dimension de la zone de contact

Dans l'équation du résultat exact, $a^{3}$ est solution d'une équation du second degré :

$a^{3}={\frac {3\,R}{4\,E^{\star }}}\,\left(F+3\pi \,R\,W+{\sqrt {6\pi \,W\,R\,F+(3\pi \,W\,R)^{2}}}\right)$

Références

(en) K.L. Johnson, K. Kendall, and A.D. Roberts., « Surface Energy and the Contact of Elastic Solids », Proc. R. Soc. Lond. Ser. A., vol. 324,‎ 1971, p. 301 (DOI 10.1098/rspa.1971.0141, lire en ligne)
(en) K. L. Johnson, Contact mechanics, Cambridge University Press, 1985 (lire en ligne)

Liens externes

: document présentant les calculs détaillés et un recueil de formules de la théorie JKR pour deux sphères.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.