Théorème de Tverberg
Le théorème de Tverberg (en anglais : Tverberg’s theorem ) est un théorème qui fait partie à la fois du domaine mathématique de la géométrie convexe et de la combinatoire topologique ; il remonte à un article publié par le mathématicien norvégien Helge Tverberg en 1966. Il représente une généralisation du théorème de Radon et est le point de départ d'un grand nombre d'investigations plus approfondies. Le théorème de Bárány est lui est étroitement lié, et le théorème de Tverberg peut en être dérivé[1] - [2] - [3].
Formulation du théorème
La théorème s'énonce comme suit[4] - [5] - [6] :
Théorème — Soient et deux entiers et . Pour tout ensemble de l'espace euclidien contenant au moins points, il existe une décomposition
en sous-ensembles disjoints deux-à-deux telle que l'intersection de leurs enveloppes convexes
est non vide.
Exemples
Pour , un ensemble de points de la droite réelle peut être réparti en sous-ensembles dont les enveloppes convexes se croisent. En effet, si les points sont , alors la partition en pour satisfait cette condition (et d'ailleurs elle est unique).
Pour , le théorème de Tverberg stipule que tout ensemble de points peut être partitionné en deux sous-ensembles dont les enveloppes convexes se croisent. Ce théorème est connu sous le nom de théorème de Radon. Dans ce cas aussi, pour des points en position générale, la partition est unique.
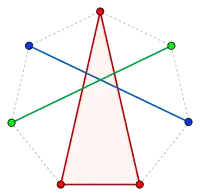
Dans le cas r = 3 et n = 2, le théorème stipule que sept points quelconques du plan peuvent être divisés en trois sous-ensembles dont les enveloppes convexes se coupent. L'illustration montre un exemple dans lequel les sept points sont les sommets d'un heptagone régulier. Comme le montre l'exemple, il peut y avoir de nombreuses partitions de Tverberg différentes du même ensemble de points ; ces sept points peuvent être partitionnés de sept façons différentes qui diffèrent par des rotations les unes des autres.
Commentaires
- Le théorème de Tverberg et été conjecturé auparavant par Bryan John Birch dans un article publié en 1959[5].
- Le théorème est optimal en ce sens que l'énoncé du théorème pour les sous-ensembles avec au plus points n'est plus valable[7].
- Comme déjà mentionné plus haut, pour , on obtient le théorème de Radon.
Théorème de Tverberg topologique
Une formulation équivalente du théorème de Tverberg est la suivante :
Un énoncé équivalent — Soient et des entiers positifs et . Soit une fonction affine d'un simplexe ; il existe des faces disjointes deux-à-deux de dont les images par s'intersectent, en d'autres termes telles que pour tout et .
Les énoncés sont équivalentes car toute fonction affine sur un simplexe est uniquement déterminée par les images de ses sommets.
Le théorème topologique de Tverberg généralise cette formulation : on prend pour une fonction continue et pas nécessairement affine. Mais l'énoncé n'est prouvé que dans le cas où est une puissance d'un nombre premier. L'énoncé est le suivant :
Théorème topologique — Soit un entier positif, soit une puissance d'un nombre premier et soit . Si est une fonction continue du simplexe de dimension , alors il existe faces deux à deux disjointes de dont les images sous se coupent. En d'autres termes, il existe des faces de telles que pour et .
Le théorème topologique de Tverberg a été prouvé pour un nombre premier par Imre Bárány, Senya B. Shlosman et András Szűcs[8]. Matousek, dans la deuxième édition de son livre, présente en 2008 une autre preuve utilisant des « deleted joins ».
Le théorème a été prouvé pour une puissance d'un nombre premier par Ozaydin[9] et ultérieurement par Volovikov[10] et par Sarkaria[11]
Bibliographie
- « The Tverberg Partition Theorem », Theorem of the day, no 107, 2005–2022 (lire en ligne, consulté le ).
- Imre Bárány et Pablo Soberón, « Tverberg's theorem is 50 years old: A survey. », Bull. Amer. Math. Soc. (N.S.), vol. 55, , p. 459–492.
- Bryan J. Birch, « On 3N points in a plane », Proceedings of the Cambridge Philosophical Society, vol. 55, , p. 289–293.
- W. A. Coppel, Foundations of Convex Geometry, Cambridge University Press, coll. « Australian Mathematical Society Lecture Series » (no 12), (ISBN 0-521-63970-0).
- Mark Longueville, A Course in Topological Combinatorics, Springer-Verlag, coll. « Universitext », (ISBN 978-1-4419-7909-4, MR 2976494).
- Jiří Matoušek, Lectures on Discrete Geometry, Springer-Verlag, coll. « Graduate Texts in Mathematics » (no 212), (ISBN 0-387-95373-6, MR 1899299).
- Jiří Matoušek, Anders Björner et Günter M. Ziegler, Using the Borsuk-Ulam theorem. Lectures on topological methods in combinatorics and geometry. Written in cooperation with Anders Björner and Günter M. Ziegler, Springer-Verlag, coll. « Universitext », , 2e éd., xii+214 (ISBN 978-3-540-00362-5, zbMATH 1234.05002).
- Helge Tverberg, « A generalization of Radon's theorem », The Journal of the London Mathematical Society, vol. 41, , p. 123-128 (MR 0187147).
- Stephan Hell, Tverberg-type theorems and the Fractional Helly property (Thèse de doctorat), Technische Universität Berlin, (DOI 10.14279/DEPOSITONCE-1464, lire en ligne)
Notes et références
- (en)/(de) Cet article est partiellement ou en totalité issu des articles intitulés en anglais « Tverberg's theorem » (voir la liste des auteurs) et en allemand « Satz von Tverberg » (voir la liste des auteurs).
- Coppel 1998, p. 68 et suiv..
- Longueville 2013, p. 106 et suiv..
- Matoušek 2002, p. 200 et suiv..
- Coppel 1998, p. 69.
- Longueville 2013, p. 106.
- Matoušek 2002, p. 200.
- Coppel 1998, p. 70.
- (en) I. Bárány, S. B. Shlosman et A. Szücs, « On a Topological Generalization of a Theorem of Tverberg », Journal of the London Mathematical Society, vol. s2-23, no 1, , p. 158-164 (DOI 10. 1112/jlms/s2-23.1.158, lire en ligne)
- Murad Ozaydin, « Equivariant Maps for the Symmetric Group », Préprint resté non publié, (lire en ligne)
- (en) A. Yu. Volovikov, « On a topological generalization of the Tverberg theorem », Mathematical Notes, vol. 59, no 3, , p. 324–326 (ISSN 1573-8876, DOI 10.1007/BF02308547, lire en ligne)
- K. S. Sarkaria, « Tverberg partitions and Borsuk-Ulam theorems », Pacific Journal of Mathematics, vol. 196, no 1, , p. 231-241 (ISSN 0030-8730, lire en ligne).



























