Théorème de Carnot (perpendiculaires concourantes)
En géométrie euclidienne, le théorème de Carnot (portant le nom de Lazare Carnot ) donne une condition nécessaire et suffisante pour que trois droites perpendiculaires aux côtés (étendus) d'un triangle soient concourantes. Ce théorème peut être considéré comme une généralisation du théorème de Pythagore.
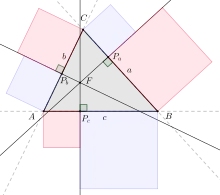
Théorème
Dans un triangle , considérons trois droites perpendiculaires en aux côtés du triangle.
Ces trois droites sont concourantes si et seulement si :
Démonstration du sens direct
Si le point de concours est F, on a d'après Pythagore : , donc ; de même, , et ; la somme des trois égalités donne la relation de Carnot.
La réciproque est démontrée dans [1].
Cas particuliers
Si le triangle est rectangle en , on peut prendre , et ; alors , , , , et . La relation du théorème de Carnot donne alors celle du théorème de Pythagore : .
Un autre corollaire est la propriété de concourance des médiatrices du triangle. Dans ce cas, on a , et , d'où la relation de Carnot ci-dessus.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Carnot's theorem (perpendiculars) » (voir la liste des auteurs).
- Mohammed AASSILA, 1000 challenges mathématiques, géométrie, Ellipses, , p. 155
Bibliographie
- (de) Mathematisch für fortgeschrittene Anfänger : Weitere beliebte Beiträge von Matroids Matheplanet, Heidelberg, Spektrum Akademischer Verlag, , 273–276 p. (ISBN 9783827426079, OCLC 699828882, lire en ligne)
- Alfred S. Posamentier et Charles T. Salkind, Challenging Problems in Geometry, New York, Dover, , 85–86 p. (ISBN 9780486134864, OCLC 829151719, lire en ligne)
Liens externes
- Florian Modler : Vergessene Sätze am Dreieck - Der Satz von Carnot sur matheplanet.com (allemand)
- Carnot's theoremt sur cut-the-knot.org





















