Théorème d'inversion de Fourier

En mathématiques, le théorème d'inversion de Fourier dit que pour de nombreux types de fonctions, il est possible de retrouver une fonction à partir de sa transformée de Fourier. En traitement du signal, on pourrait dire que la connaissance de toutes les informations d'amplitude et de phase des ondes constituant un signal permet précisément de reconstruire ce signal.

Le théorème dit que si nous avons une fonction $f:\mathbb {R} \to \mathbb {C}$ satisfaisant certaines conditions, on peut définir la transformée de Fourier comme

({\mathcal {F}}f)(\xi ):=\int _{\mathbb {R} }\mathrm {e} ^{-2\pi \mathrm {i} y\cdot \xi }\,f(y)\,\mathrm {d} y,

et la reconstruction de $f$ à partir de sa transformée

f(x)=\int _{\mathbb {R} }\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }\,({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi .

En d'autres termes, le théorème d'inversion de Fourier dit que

f(x)=\iint _{\mathbb {R} ^{2}}\mathrm {e} ^{2\pi \mathrm {i} (x-y)\cdot \xi }\,f(y)\,\mathrm {d} y\,\mathrm {d} \xi .

Une autre façon d'énoncer le théorème est que si $R$ est l'opérateur défini par $(Rf)(x):=f(-x)$ , alors

{\mathcal {F}}^{-1}={\mathcal {F}}R=R{\mathcal {F}}.

Le théorème est vérifié si la fonction $f$ et sa transformée de Fourier sont absolument intégrables (au sens de Lebesgue) et si $f$ est continue au point $x$ . Cependant, même dans des conditions plus générales, les versions du théorème d'inversion de Fourier restent valables. Dans ces cas, les intégrales ci-dessus peuvent ne pas converger dans un sens ordinaire.

Propriétés

Dans cette section, on suppose que $f$ est une fonction continue intégrable. Sa transformée de Fourier est donnée par

({\mathcal {F}}f)(\xi ):=\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-2\pi \mathrm {i} y\cdot \xi }\,f(y)\,\mathrm {d} y.

De plus, on suppose que la transformée de Fourier ${\mathcal {F}}f$ est également intégrable.

Transformée de Fourier inverse en tant qu'intégrale

L'énoncé le plus courant du théorème d'inversion de Fourier est de donner la transformée inverse comme une intégrale. Pour toute fonction intégrable $g$ et tout $x\in \mathbb {R} ^{n}$ ensemble

{\mathcal {F}}^{-1}g(x):=\int _{\mathbb {R} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }\,g(\xi )\,\mathrm {d} \xi .

Alors pour tous $x\in \mathbb {R} ^{n}$ on a

{\mathcal {F}}^{-1}({\mathcal {F}}f)(x)=f(x).

Théorème d'inversion de Fourier

Le théorème peut être reformulé comme

f(x)=\int _{\mathbb {R} ^{n}}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} (x-y)\cdot \xi }\,f(y)\,\mathrm {d} y\,\mathrm {d} \xi .

Si $f$ est une fonction à valeurs réelles, alors en prenant la partie réelle de chaque côté de ce qui précède, il vient :

f(x)=\int _{\mathbb {R} ^{n}}\int _{\mathbb {R} ^{n}}\cos(2\pi (x-y)\cdot \xi )\,f(y)\,\mathrm {d} y\,\mathrm {d} \xi .

Transformation inverse à l'aide de l'opérateur d'inversion d'espace

Pour toute fonction $g$ on définit l'opérateur d'inversion d'espace ${\mathcal {R}}$ par

{\mathcal {R}}g(x):=g(-x).

Ensuite, on peut alors redéfinir la transformée de Fourier inverse par

{\mathcal {F}}^{-1}f:={\mathcal {R}}{\mathcal {F}}f={\mathcal {F}}{\mathcal {R}}f.

Il est immédiat à partir de la définition de la transformée de Fourier et de l'opérateur d'inversion que les deux fonctions ${\mathcal {R}}{\mathcal {F}}f$ et ${\mathcal {F}}{\mathcal {R}}f$ correspondent à la définition de ${\mathcal {F}}^{-1}f$ , et en particulier sont égaux entre eux et satisfont ${\mathcal {F}}^{-1}({\mathcal {F}}f)(x)=f(x)$ .

Depuis ${\mathcal {R}}f={\mathcal {R}}{\mathcal {F}}^{-1}{\mathcal {F}}f={\mathcal {RR}}{\mathcal {FF}}f$ on a ${\mathcal {R}}={\mathcal {F}}^{2}$ et

{\mathcal {F}}^{-1}={\mathcal {F}}^{3}.

Conditions d'application du théorème

Lorsqu'il est utilisé en physique et en ingénierie, le théorème d'inversion de Fourier est souvent utilisé sous l'hypothèse que tout « se comporte bien ». En mathématiques, de tels arguments heuristiques ne sont pas autorisés, et le théorème d'inversion de Fourier inclut une spécification explicite de la classe de fonctions autorisée. Cependant, il n'y a pas de "meilleure" classe de fonctions à considérer donc plusieurs variantes du théorème d'inversion de Fourier existent, bien qu'avec des conclusions compatibles.

Fonctions de Schwartz

Le théorème d'inversion de Fourier est valable pour toutes les fonctions de Schwartz (en gros, les fonctions lisses qui décroissent rapidement et dont toutes les dérivées décroissent rapidement à l'infini). Cette condition a l'avantage d'imposer des conditions uniquement sur la fonction (par opposition à imposer une condition sur sa transformée de Fourier), et l'intégrale qui définit la transformée de Fourier et son inverse sont absolument intégrables. Cette version du théorème est utilisée dans la preuve du théorème d'inversion de Fourier pour les distributions tempérées (voir ci-dessous).

Fonctions intégrables avec transformée de Fourier intégrable

Le théorème d'inversion de Fourier est valable pour toutes les fonctions continues qui sont absolument intégrables (c'est-à-dire appartenant à $L^{1}(\mathbb {R} ^{n})$ ) et dont la transformée de Fourier est absolument intégrable. Cela inclut toutes les fonctions de Schwartz, c'est donc une forme strictement plus forte du théorème que la précédente mentionnée.

Une légère variante consiste à abandonner la condition que la fonction $f$ soit continue mais à exiger qu'elle et sa transformée de Fourier soient absolument intégrables. Dans ce cas, on a $f = g$ presque partout où $g$ est une fonction continue, et ${\mathcal {F}}^{-1}({\mathcal {F}}f)(x)=g(x)$ pour chaque $x\in \mathbb {R} ^{n}$ .

Fonctions intégrables d'une seule variable

Fonctions d'une seule variable régulières par morceaux

Si la fonction est absolument intégrable en une dimension (c'est-à-dire $f\in L^{1}(\mathbb {R} )$ ) et est lisse par morceaux alors une version du théorème d'inversion de Fourier est vérifiée. Dans ce cas on définit

{\mathcal {F}}^{-1}g(x):=\lim _{R\to \infty }\int _{-R}^{R}\mathrm {e} ^{2\pi \mathrm {i} x\xi }\,g(\xi )\,\mathrm {d} \xi .

Alors pour tous $x\in \mathbb {R}$

{\mathcal {F}}^{-1}({\mathcal {F}}f)(x)={\frac {1}{2}}(f(x_{-})+f(x_{+})),

c'est-à-dire ${\mathcal {F}}^{-1}({\mathcal {F}}f)(x)$ est égal à la moyenne des limites gauche et droite de $f$ à $x$ . Aux points où $f$ est continue, on retrouve $f (x)$ .

Une généralisation en dimension supérieure de cette forme du théorème est également valable, mais selon Folland (1992) c'est « plutôt délicat et pas très utile ».

Fonctions d'une seule variable continues par morceaux

Si la fonction est absolument intégrable en une dimension (c'est-à-dire $f\in L^{1}(\mathbb {R} )$ ) mais simplement continue par morceaux, alors une version du théorème d'inversion de Fourier est toujours valable. Dans ce cas, l'intégrale dans la transformée de Fourier inverse est définie à l'aide d'une fonction de coupure régulière ; nous définissons spécifiquement

{\mathcal {F}}^{-1}g(x):=\lim _{R\to \infty }\int _{\mathbb {R} }\varphi (\xi /R)\,\mathrm {e} ^{2\pi \mathrm {i} x\xi }\,g(\xi )\,\mathrm {d} \xi ,\qquad \varphi (\xi ):=\mathrm {e} ^{-\xi ^{2}}.

La conclusion du théorème est alors la même que pour le cas régulier par morceaux discuté ci-dessus.

Fonctions de plusieurs variables continues

Si $f$ est continue et absolument intégrable sur $\mathbb {R} ^{n}$ alors le théorème d'inversion de Fourier est toujours valable en redéfinissant la transformée inverse avec une fonction de coupure régulière, c'est-à-dire

{\mathcal {F}}^{-1}g(x):=\lim _{R\to \infty }\int _{\mathbb {R} ^{n}}\varphi (\xi /R)\,\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }\,g(\xi )\,\mathrm {d} \xi ,\qquad \varphi (\xi ):=\mathrm {e} ^{-\vert \xi \vert ^{2}}.

La conclusion est maintenant simplement que pour tous $x\in \mathbb {R} ^{n}$

{\mathcal {F}}^{-1}({\mathcal {F}}f)(x)=f(x).

Fonctions de plusieurs variables sans condition de régularité

En abandonnant toute hypothèse sur la continuité (par morceaux) de $f$ et pour ne supposer que l'intégrabilité absolue, alors une version du théorème est toujours valable. La transformée inverse est à nouveau définie avec la coupure régulière, mais avec la conclusion que

{\mathcal {F}}^{-1}({\mathcal {F}}f)(x)=f(x)

pour presque tous $x\in \mathbb {R} ^{n}.$ [1]

Fonctions de carré intégrable

Dans ce cas, la transformée de Fourier ne peut pas être définie directement comme une intégrale car elle peut ne pas être absolument convergente, elle est donc définie par un argument de densité (voir Transformation de Fourier). Par exemple, on considère :

g_{k}(\xi ):=\int _{\{y\in \mathbb {R} ^{n}:\left\vert y\right\vert \leq k\}}\mathrm {e} ^{-2\pi \mathrm {i} y\cdot \xi }\,f(y)\,\mathrm {d} y,\qquad k\in \mathbb {N} ,

On peut définir ${\textstyle {\mathcal {F}}f:=\lim _{k\to \infty }g_{k}}$ où la limite est prise au sens de la norme $L 2$ . La transformée inverse peut être définie par la densité de la même manière ou en la définissant en termes de transformée de Fourier et de l'opérateur d'inversion. On a alors

f(x)={\mathcal {F}}({\mathcal {F}}^{-1}f)(x)={\mathcal {F}}^{-1}({\mathcal {F}}f)(x)

au sens de la norme $L 2$ . En dimension 1 (et seulement dans ce cas), on peut également montrer que l'intégrale converge pour presque tout $x \in ℝ$ — c'est le théorème de Carleson, mais c'est beaucoup plus difficile à prouver que la convergence en norme $L 2$ .

Distributions tempérées

La transformée de Fourier peut être définie sur l'espace des distributions tempérées ${\mathcal {S}}'(\mathbb {R} ^{n})$ par dualité de la transformée de Fourier sur l'espace des fonctions de Schwartz. Spécifiquement pour $f\in {\mathcal {S}}'(\mathbb {R} ^{n})$ et pour toutes les fonctions de test $\varphi \in {\mathcal {S}}(\mathbb {R} ^{n})$ (espace de Schwartz) on pose

{\displaystyle \langle {\mathcal {F}}f,\varphi \rangle

où ${\mathcal {F}}\varphi$ est défini à l'aide de la formule intégrale. Si $f\in L^{1}(\mathbb {R} ^{n})\cap L^{2}(\mathbb {R} ^{n})$ alors on retrouve la définition habituelle. On peut définir la transformée inverse ${\mathcal {F}}^{-1}\colon {\mathcal {S}}'(\mathbb {R} ^{n})\to {\mathcal {S}}'(\mathbb {R} ^{n})$ , soit par dualité à partir de la transformation inverse sur les fonctions de Schwartz de la même manière, soit en la définissant à l'aide de l'opérateur d'inversion (où celui-ci est défini par dualité). On a alors

{\mathcal {F}}{\mathcal {F}}^{-1}={\mathcal {F}}^{-1}{\mathcal {F}}=\operatorname {Id} _{{\mathcal {S}}'(\mathbb {R} ^{n})}.

Relation avec les séries de Fourier

Lorsque l'on considère la série de Fourier d'une fonction périodique, à une transformation linéaire près, il est classique de considérer la fonction $2 π$ périodique. Dans cette section, on utilisera plutôt la convention d'avoir $f$ de période 1, agissant sur l'intervalle $[0;1]$ , car cela correspond à la convention de la transformée de Fourier utilisée ici.

Le théorème d'inversion de Fourier est analogue à la convergence des séries de Fourier. Dans le cas de la transformée de Fourier, on a

f\colon \mathbb {R} ^{n}\to \mathbb {C} ,\quad {\hat {f}}\colon \mathbb {R} ^{n}\to \mathbb {C} ,

{\hat {f}}(\xi ):=\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-2\pi \mathrm {i} y\cdot \xi }\,f(y)\,\mathrm {d} y,

f(x)=\int _{\mathbb {R} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }\,{\hat {f}}(\xi )\,\mathrm {d} \xi .

Dans le cas de la série de Fourier, on a plutôt

f\colon [0,1]^{n}\to \mathbb {C} ,\quad {\hat {f}}\colon \mathbb {Z} ^{n}\to \mathbb {C} ,

{\hat {f}}(k):=\int _{[0,1]^{n}}\mathrm {e} ^{-2\pi \mathrm {i} y\cdot k}\,f(y)\,\mathrm {d} y,

f(x)=\sum _{k\in \mathbb {Z} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} x\cdot k}\,{\hat {f}}(k).

Applications

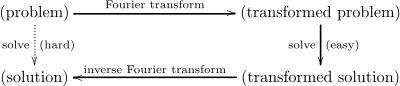
Certains problèmes, comme la résolution d'équations différentielles, deviennent plus faciles à résoudre lorsque la transformée de Fourier est appliquée. Dans ce cas, la solution du problème d'origine est récupérée en utilisant la transformée de Fourier inverse.

Dans les applications de la transformée de Fourier, le théorème d'inversion de Fourier joue souvent un rôle critique. Dans de nombreuses situations, la stratégie de base consiste à appliquer la transformée de Fourier, à effectuer une opération ou une simplification, puis à appliquer la transformée de Fourier inverse.

De manière plus abstraite, le théorème d'inversion de Fourier est une propriété de la transformée de Fourier en tant qu'opérateur (voir Transformée de Fourier sur les espaces de fonctions ). Par exemple, le théorème d'inversion de Fourier sur $f\in L^{2}(\mathbb {R} ^{n})$ montre que la transformée de Fourier est un opérateur unitaire sur $L^{2}(\mathbb {R} ^{n})$ .

Propriétés de la transformée inverse

La transformée de Fourier inverse est extrêmement similaire à la transformée de Fourier d'origine : comme indiqué ci-dessus, elle ne diffère que par l'application d'un opérateur d'inversion. Pour cette raison, les propriétés de la transformée de Fourier sont valables pour la transformée de Fourier inverse, comme le théorème de convolution et le lemme de Riemann-Lebesgue .

Des tables de transformées de Fourier peuvent facilement être utilisées pour la transformée de Fourier inverse en composant la fonction recherchée avec l'opérateur d'inversion. Par exemple, en regardant la transformée de Fourier de la fonction porte, on a

f(x)=\operatorname {rect} (ax)\quad \Rightarrow \quad ({\mathcal {F}}f)(\xi )={\frac {1}{|a|}}\operatorname {sinc} \left({\frac {\xi }{a}}\right)\!,

que l'on réécrit pour faire apparaître la transformée inverse

g(\xi )=\operatorname {rect} (a\xi )\quad \Rightarrow \quad ({\mathcal {F}}^{-1}g)(x)={\frac {1}{|a|}}\operatorname {sinc} \left(-{\frac {x}{a}}\right)\!.

Preuve

Etant donné la fonction $f (y)$ et sa transformée ${\mathcal {F}}f(\xi )=\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-2\pi \mathrm {i} y\cdot \xi }f(y)\,\mathrm {d} y$ , voici quelques résultats intermédiaires

Si $x\in \mathbb {R} ^{n}$ et $g(\xi )=\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }\psi (\xi )$ , alors $({\mathcal {F}}g)(y)=({\mathcal {F}}\psi )(y-x)$ .
Si $\varepsilon \in \mathbb {R}$ et $\psi (\xi )=\varphi (\varepsilon \xi )$ , alors $({\mathcal {F}}\psi )(y)=({\mathcal {F}}\varphi )(y/\varepsilon )/|\varepsilon |$ .
Pour $f,g\in L^{1}(\mathbb {R} ^{n})$ , le théorème de Fubini implique que $\textstyle \int g(\xi )\cdot ({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi =\int ({\mathcal {F}}g)(y)\cdot f(y)\,\mathrm {d} y$ .
Soit $\varphi (\xi )=\mathrm {e} ^{-\pi \vert \xi \vert ^{2}}$ ; alors $({\mathcal {F}}\varphi )(y)=\varphi (y)$ .
Soit $\varphi _{\varepsilon }(y)=\varphi (y/\varepsilon )/\varepsilon ^{n}$ . Le symbole $\ast$ désignant le produit de convolution, $\varphi _{\varepsilon }$ est une approximation de l'identité : pour toute fonction continue $f\in L^{1}(\mathbb {R} ^{n})$ et pour tout $x\in \mathbb {R} ^{n}$ , on a la limite $\lim _{\varepsilon \to 0}(\varphi _{\varepsilon }\ast f)(x)=f(x)$ (où la convergence est ponctuelle).

Puisque, par hypothèse, ${\mathcal {F}}f\in L^{1}(\mathbb {R} ^{n})$ , alors il s'ensuit par le théorème de convergence dominée que

\int _{\mathbb {R} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi =\lim _{\varepsilon \to 0}\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-\pi \varepsilon ^{2}|\xi |^{2}+2\pi \mathrm {i} x\cdot \xi }({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi .

Soit $g_{x}(\xi )=\mathrm {e} ^{-\pi \varepsilon ^{2}\vert \xi \vert ^{2}+2\pi \mathrm {i} x\cdot \xi }$ . En appliquant les résultats 1, 2 et 4, à plusieurs reprises pour des intégrales multiples si nécessaire, on obtient

({\mathcal {F}}g_{x})(y)={\frac {1}{\varepsilon ^{n}}}\mathrm {e} ^{-{\frac {\pi }{\varepsilon ^{2}}}|x-y|^{2}}=\varphi _{\varepsilon }(x-y).

En utilisant la propriété 3 sur $f$ et $g x$ , pour chaque $x\in \mathbb {R} ^{n}$ , on a

\int _{\mathbb {R} ^{n}}\mathrm {e} ^{-\pi \varepsilon ^{2}|\xi |^{2}+2\pi \mathrm {i} x\cdot \xi }({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi =\int _{\mathbb {R} ^{n}}{\frac {1}{\varepsilon ^{n}}}\mathrm {e} ^{-{\frac {\pi }{\varepsilon ^{2}}}|x-y|^{2}}f(y)\,\mathrm {d} y=(\varphi _{\varepsilon }*f)(x),

le produit de convolution de $f$ avec une forme approchée de l'identité. Mais puisque $f\in L^{1}(\mathbb {R} ^{n})$ , le résultat 5 dit que

\lim _{\varepsilon \to 0}(\varphi _{\varepsilon }*f)(x)=f(x).

En rassemblant ce qui précède, nous avons montré que

\int _{\mathbb {R} ^{n}}\mathrm {e} ^{2\pi \mathrm {i} x\cdot \xi }({\mathcal {F}}f)(\xi )\,\mathrm {d} \xi =f(x).\qquad \square

Références

[[Gerald Folland (en)|G. B. Folland]], Fourier Analysis and its Applications, Belmont, CA, USA, Wadsworth, 1992 (ISBN 0-534-17094-3)
[[Gerald Folland (en)|G. B. Folland]], Introduction to Partial Differential Equations, Princeton, USA, Princeton Univ. Press, 1995 (ISBN 978-0-691-04361-6)

(en-US) « DMat0101, Notes 3: The Fourier transform on L^1 », I Woke Up In A Strange Place,‎ 10 mars 2011 (lire en ligne, consulté le 12 février 2018)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.