Tache d'Airy

On doit la description du phénomène à George Biddell Airy en 1835[1] alors que le phénomène de diffraction avait déjà été découvert plus d'une dizaine d'années auparavant.

Coupe de l'éclairement en fonction de la position dans une tache d'Airy.

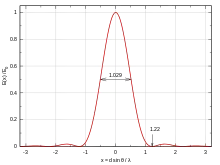
Lorsque la figure est observée loin du trou diffractant, l'éclairement varie en fonction de l'angle θ entre le point considéré et le centre de la figure[2] :

${\displaystyle E(x)=E_{0}\left({\frac {2J_{1}(\pi x)}{\pi x}}\right)^{2}}$,

où

• ${\displaystyle x={\frac {d\sin \theta }{\lambda }}}$,
• ${\displaystyle E_{0}}$ est l'éclairement au centre de la figure ;
• ${\displaystyle J_{1}}$ est la fonction de Bessel du premier ordre ;
• ${\displaystyle d}$ est le diamètre de l'ouverture ;
• ${\displaystyle \theta }$ est l'angle, ayant son sommet au centre du trou, entre l'axe de révolution et la direction considérée ;
• ${\displaystyle \lambda }$ est la longueur d'onde de la lumière.

Cette expression est obtenue par la théorie de la diffraction de Fraunhofer. Elle correspond au carré du module de la transformée de Fourier de la fonction caractéristique du disque représentant l'ouverture.

La première annulation de cette fonction se produit lorsque ${\displaystyle x\simeq 1{,}22}$ ce qui correspond à un angle

${\displaystyle \theta \simeq 1{,}22\,{\frac {\lambda }{d}}}$.

La figure de diffraction peut aussi être observée à plus courte distance en se plaçant dans le plan focal d'un objectif. C'est notamment le cas lorsqu'on considère la diffraction provoquée par l'ouverture de ce même objectif. On a alors la même expression de ${\displaystyle E(x)}$, où l'on peut écrire :

${\displaystyle x={\frac {d}{\lambda }}\sin \theta ={\frac {d}{\lambda }}{\frac {r}{f}}={\frac {r}{N\lambda }}}$,

où

• ${\displaystyle r}$ est la distance entre le point considéré sur l'image et le centre de la figure ;
• ${\displaystyle f}$ est la focale de l'objectif ;
• ${\displaystyle N}$ est son nombre d'ouverture.

Le rayon du premier disque noir constitue le rayon de la tache d'Airy et vaut :

${\displaystyle r\simeq 1{,}22\,\lambda \,N}$.

Un effet important de cette tache, est la dégradation de la résolution des images dans les appareils optiques (appareil photographique, télescope…). On peut calculer le critère de Rayleigh avec ce profil de la tache d'Airy, donnant une formule de la limite de séparation entre deux objets. Des techniques numériques de traitement d'image, comme la déconvolution, permettent de compenser en partie ce phénomène d'étalement du signal.

La tache d'Airy intervient aussi lors de la lecture d'un espace de stockage optique (CD, DVD, blu-ray...). En effet, la capacité de stockage de ces supports optiques est entièrement dépendante de la largeur de cette tache : la tache ne doit couvrir qu'une seule piste du disque, ainsi, plus la tache est large, plus l'espace entre deux pistes est grand, et moins la capacité de stockage est grande.

• Optique physique
• Théorie de la diffraction
• Fonction d'étalement du point

Démonstration sur le site de l'Observatoire de Paris