Tétrahémihexaèdre
En géométrie, le tétrahémihexaèdre, appelé aussi heptaèdre de Reinhardt (du nom de Curt Reinhardt[note 1], qui l'a inventé en 1885[1]) est un polyèdre uniforme non convexe, indexé sous le nom U4.
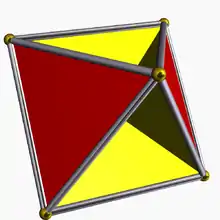
| Faces | Arêtes | Sommets |
|---|---|---|
| 7 (4 triangles, 3 carrés) | 12 | 6 de degré 3 |
| Type | Polyèdre étoilé uniforme |
|---|---|
| Références d'indexation | U4 – C36 – W67 |
| Symbole de Wythoff | 32 3 | 2 |
| Caractéristique | 1 |
| Groupe de symétrie | Td |
Description
Il a 6 sommets, 12 arêtes, et 7 faces : 4 triangulaires (qui font partie de celles de l'octaèdre régulier) et 3 carrées.
C'est le seul polyèdre uniforme non prismatique avec un nombre impair de faces. Il est le seul polyèdre uniforme avec une caractéristique d'Euler égale à 1 et est par conséquent une représentation du plan projectif réel très similaire à la surface romaine.
La partie « hémi » du nom vient du fait que certaines faces (ici : les faces carrées) sont en nombre moitié (ici : trois) du polyèdre régulier associé (ici : l'hexaèdre, c'est-à-dire le cube). Elles passent par le centre, et sont (comme dans le cube) perpendiculaires.
Notes et références
Notes
- Curt Reinhardt (1855-1940), philosophe et mathématicien de l'université de Leipzig, ayant étudié les travaux de Mobius et auteur d'une Introduction à la théorie des polyèdres - voir sa fiche worldcat
Références
- « Tétrahémihexaèdre », sur mathcurve.com.
Liens externes
- Patron en papier sur software3d.com
- (en) Eric W. Weisstein, « Tetrahemihexahedron », sur MathWorld