Télécorrélation atmosphérique

Le terme « téléconnexion » a été introduit en 1981 par deux chercheurs américains, Wallace et Gutzler, pour désigner un effet climatique récurrent résultant d'un forçage (changement de température, pression, etc.) distant[1]. Le terme est ambivalent en français alors que l'on peut penser aux interconnexions dans les télécommunications, c'est pourquoi le terme « télécorrélation atmosphérique » est plus approprié[2].

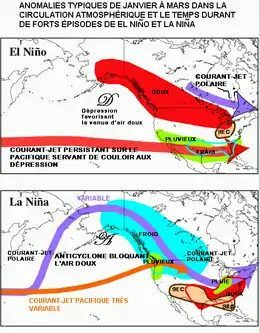
Un exemple de ce concept est la phase d'El Niño-Oscillation australe (ENSO) dans le Pacifique tropical qui a un impact sur les précipitations en Californie, dans certaines parties de l'Australie, de l'Afrique du Sud et de l'Amérique du Sud[3]. Plusieurs autres modes climatiques tels que l'oscillation de Madden-Julian (OMJ), l'oscillation nord-atlantique (ONA), l'oscillation quasi-biennale (OQB), le dipôle de l'océan Indien (DOI) et l'oscillation décennale du Pacifique (ODP) ont été décrits, et leurs interconnexions ainsi que leurs impacts à distance ont été largement étudiés à l'aide d'observations, de modèles climatiques et de la théorie physique.

Étant donné que la température de surface de la mer en zone tropicale est prévisible jusqu'à deux ans à l'avance, la connaissance des modèles de télécorrélation donne une certaine prévisibilité dans des endroits éloignés avec des perspectives parfois aussi longues que quelques saisons[3]. Par exemple, la prévision d'El Niño permet de prévoir les précipitations, les chutes de neige, les sécheresses ou les modèles de température en Amérique du Nord avec un délai de quelques semaines à quelques mois. À l'époque de Sir Gilbert Walker, un fort El Niño signifiait généralement une mousson indienne plus faible, mais cette anticorrélation s'est affaiblie dans les années 1980 et 1990.

Les télécorrélations ont été notées pour la première fois par le météorologue britannique Sir Gilbert Walker à la fin du XIX^e siècle grâce au calcul de la corrélation entre les séries chronologiques de la pression atmosphérique, de la température et des précipitations. Ils ont servi de base à la compréhension de la variabilité climatique en montrant que celle-ci n'était pas purement aléatoire dans le cas de l'ENSO. Ce phénomène a des effets dans plusieurs endroits à la fois, même en Amérique du Nord.

Dans les années 1980, des observations améliorées ont permis la détection de télécorrélations à de plus grandes distances dans toute la troposphère[4]. Simultanément, la théorie a émergé selon laquelle de tels modèles pourraient être compris à travers la dispersion des ondes de Rossby en raison de la géométrie sphérique de la Terre[5]. Ceci est parfois appelé le « proto-modèle »[6].

Les télécorrélations au sein du Pacifique tropical ont commencé à être comprises grâce aux calculs idéalisés d'A. E. Gill et plus tard à travers des modèles plus complexes[7]. S'appuyant sur le proto-modèle, une grande partie de la première théorie des télécorrélations traitait d'un modèle barotrope linéarisé de l'écoulement atmosphérique autour d'un état moyen constant. Ce modèle a été rapidement invalidé lorsqu'il a été découvert que les télécorrélations réelles étaient presque insensibles à l'emplacement du forçage, en contradiction directe avec les prédictions offertes. Simmons et ses collaborateurs ont ensuite montré que si un état initial plus réaliste était utilisé, il deviendrait instable, conduisant à un schéma similaire quel que soit l'emplacement du forçage, conformément aux observations[8]. Cette propriété modale s'est avérée être un artefact de la barotropie du modèle, bien qu'elle soit apparue pour des raisons plus subtiles dans des modèles plus réalistes.

Des travaux plus récents ont montré que la plupart des télécorrélations des tropicales et extratropicales peuvent être comprises avec une précision surprenante par la propagation d'ondes planétaires linéaires sur un état de base tridimensionnel variant selon les saisons[9]. Parce que les modèles sont persistants dans le temps et quelque peu contraints par caractéristiques géographiques telles que les chaînes de montagnes, ces ondes sont appelées stationnaires.

Un autre mécanisme de télécorrélation entre les océans tropicaux et les régions de latitude moyenne est symétrique le long des cercles de latitude (c'est-à-dire zonal) et entre les hémisphères, contrairement au mécanisme des ondes stationnaires. Il repose sur des interactions entre les tourbillons transitoires et le flux atmosphérique moyen qui se renforcent mutuellement (c'est-à-dire effets non-linéaires). Il a été démontré qu'il expliquait certains aspects des télécorrélations ENSO en termes de température et de précipitations[10] - [11]. D'autres auteurs ont également suggéré une corrélation entre de nombreux schémas de télécorrélation et des facteurs locaux de variation climatique[12].