Signature de cercle
La signature de cercle (en anglais : Ring signature), aussi appelé signature d’anneau, est un procédé cryptographique permettant à une personne de signer électroniquement de façon anonyme un message ou un document au nom d’un « cercle ». Les membres de ce cercle sont choisis par l’auteur de la signature et ne sont pas nécessairement informés de leur implication dans la création de la signature électronique. La seule contrainte est qu’ils doivent tous avoir une clef cryptographique publique.
La signature de cercle a donné lieu à un dérivé: la signature de cercle à seuil, où la signature est initiée par un nombre prédéfini de membres du cercle.
Principe
Comme l'indique le titre de l'article où elle est décrite pour la première fois, How to Leak a Secret[1], le but premier de cette signature est de permettre la fuite d'information.
Dans cet article est donné l'exemple d'un membre d'un cabinet ministériel voulant donner à un journaliste des informations sur le premier ministre. Il ne désire évidemment pas divulguer son identité, mais souhaite que le journaliste sache que la fuite vient du cabinet et non pas d'un plaisantin. La signature de cercle lui permet ainsi de signer en tant que membre du cabinet ministériel, et non en tant qu'individu, sans que ses collègues soient au courant, ni que quiconque puisse remonter à lui, contrairement à la signature de groupe qui impose une coopération des membres inclus dans la signature et la possibilité pour une personne déterminée à l'initialisation de connaître l'identité du signataire.
Une autre utilisation proposée dans cet article est celle permettant de générer une signature qui n'aura de valeur que pour le destinataire. Ainsi la source envoie un document signé à l'aide d'une signature de cercle comprenant sa clef et celle du destinataire. Ce dernier, sachant qu'il ne l'a pas produit, a donc la preuve que le message provient bien de la source. Mais s'il montre le document à un tiers, ce dernier ne peut pas être sûr que le message n'est pas un faux, créé par le destinataire.
Définition
Une signature d’anneau[2] est définie comme étant la donnée de quatre algorithmes, certains similaires à ceux d’une signature numérique: (Init, Gén, Signer, Vérifier). Ceux-ci fonctionnent de la manière suivante :
- L'initialisation Init prend en entrée un paramètre de sécurité et renvoie une chaîne de référence commune ρ.
- La génération de clefs Gén, qui est lancée par l'utilisateur, prend en entrée la chaîne de référence commune, et renvoie un couple de clefs : une clef de vérification vk, et une clef de signature sk.
- La signature Signer prend en entrée la clef de signature sk, la chaîne de référence commune, le message à signer, un ensemble R de clefs de vérification telle que celle associée à la clef de signature sk y appartient. Et cet algorithme renvoie une signature σ.
- La vérification Vérifier prend en entrée la chaîne de référence commune, un ensemble R de clefs de vérifications, un message M et une signature σ, et renvoie accepte ou rejette.
Ces algorithmes vont de pair avec des notions de sécurité associés, qui sont la correction de la signature, qui spécifie que si une signature est honnêtement générée, alors elle sera toujours acceptée. La non-falsifiabilité, qui requiert que sans posséder de clefs privée associée à un des éléments de l'ensemble R, il est impossible de concevoir une signature valide, et l’anonymat, qui dit qu'il est impossible de lier une signature à son signataire.
Le schéma de Rivest, Shamir et Tauman
Dans cette partie, une description du schéma proposé par Rivest, Shamir et Tauman[1] est donnée.
Dans ce schéma, l'utilisateur génère une signature σ pour le message M à signer, un aléa v, son couple clef privée/publique et les clefs publiques des autres membres du cercle R = (pki)i ∈ [1;n]. De plus ce schéma dépend d’un schéma de chiffrement (Enc, Dec).
Les utilisateurs peuvent ainsi vérifier cette signature à l'aide de σ, M, v et de l'ensemble des clefs publiques impliquées dans le processus de création.
Signature
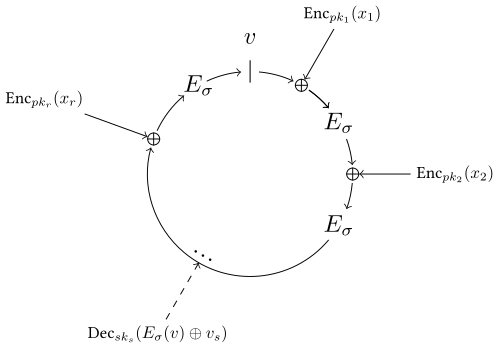
Le signataire génère un haché σ du message M et choisit ensuite un nonce v0. Pour chaque clef publique pki ∈ R autre que la sienne, le signataire choisit une valeur xi aléatoirement, la chiffre avec la clef publique pki et effectue une disjonction exclusive du résultat avec la valeur v avant d'appliquer une permutation symétrique Eσ au résultat, ce qui donnera une nouvelle valeur « vi ».
Ce qui donne itérativement : vi := Eσ (Encpki(xi) ⊕ vi-1)
On recommence la manipulation avec les autres clefs publiques.
À la fin, on se retrouve avec une valeur v = vn. On recherche alors la valeur y qui, mise en ou exclusif avec le v trouvé et permuté avec Eσ, permet de retrouver v0. Autrement dit v0 = Eσ(y ⊕ v). On utilise enfin la clef privée pour retrouver l'antécédent de y par le chiffrement, c'est-à-dire x = Decsk(y).
Finalement la signature renvoyée sera Σ = (v, (xi)i)
Vérification
Le destinataire refait les calculs vi = Eσ (f (xi) ⊕ vi+1) pour toutes les clefs publiques de la signature et vérifie qu'il retrouve bien le v original à la fin.
La taille de la signature est linéaire en N, qui correspond à la taille du cercle, car il faut spécifier les aléas xi utilisées par chaque participants.
Preuve de concept
Ci-suit une preuve de concept implantée en Python ou Python3 du papier original, utilisant RSA comme cryptosystème asymétrique. Le cercle contient quatre membres.
import os, hashlib, random, functools, Crypto.PublicKey.RSA
class ring:
def __init__(self, k, l=2048):
self.k, self.l, self.n, self.q = k, l, len(k), 1 << l - 1
def sign(self, m, z):
self.permut(m)
s, u = [None]*self.n, random.randint(0, self.q)
c = v = self.E(u)
for i in list(range(z+1, self.n)) + list(range(z)):
s[i] = random.randint(0, self.q)
v = self.E(v^self.g(s[i], self.k[i].e, self.k[i].n))
if (i+1) % self.n == 0: c = v
s[z] = self.g(v^u, self.k[z].d, self.k[z].n)
return [c, ] + s
def verify(self, m, X):
self.permut(m)
y = [self.g(X[i+1], self.k[i].e, self.k[i].n) for i in range(len(X)-1)]
return functools.reduce(lambda x, i:self.E(x^y[i]), range(self.n), X[0]) == X[0]
def permut(self, m):
self.p = int(hashlib.sha1(m.encode('utf8')).hexdigest(), 16)
def E(self, x):
return int(hashlib.sha1(('%s%s'% (x, self.p)).encode('utf8')).hexdigest(), 16)
def g(self, x, e, n):
q, r = divmod(x, n)
return q*n + pow(r, e, n) if (q+1)*n <= (1<<self.l)-1 else x
if __name__ == '__main__':
size, msg1, msg2 = 4, 'hello', 'world!'
r = ring([Crypto.PublicKey.RSA.generate(2048, os.urandom) for x in range(size)])
for i in range(size):
s1, s2 = r.sign(msg1, i), r.sign(msg2, i)
assert r.verify(msg1, s1) and r.verify(msg2, s2) and not r.verify(msg1, s2)
Autres Schémas
Par la suite, d'autres schémas ont été conçus, dont celui de Dodis, Kiayias, Nicolosi et Shoup[3], qui propose un schéma à signatures de taille constante en le nombre d'utilisateurs en utilisant des accumulateurs et le schéma d'authentification de Fiat-Shamir. Une autre version, dans le modèle standard, possédant une taille qui croît comme la racine carrée du nombre d'utilisateurs (O(√N)) a été proposée par Chandran, Groth et Sahai[4].
Cryptomonnaies
La technologie Cryptonote[5] utilise des signatures de cercles. Celle-ci est utilisée dans des crypto-monnaies comme Monero, Bytecoin ou DarkNote.
Le principe de signature d’anneau a également été portée sur ShadowCash[6], une crypto-monnaie inspirée de Bitcoin.
Notes et références
Bibliographie
- [Bender, Katz et Morselli 2006] (en) Adam Bender, Jonathan Katz et Ruggero Morselli, « Ring signatures: Stronger definitions, and constructions without random oracles », TCC, , p. 60−79
- [Chandran, Groth et Sahai 2007] (en) Nishanth Chandran, Jens Groth et Amit Sahai, « Ring signatures of sub-linear size without random oracles », Automata, Languages, Programming,
- [Dodis, Kiayias, Nicolosi et Shoup 2004] (en) Yevgeniy Dodis, Aggelos Kiayias, Antonio Nicolosi et Victor Shoup, « Anonymous Identification in ad-hoc Groups », Eurocrypt, lNCS, vol. 3027,
- [Rivest, Shamir et Tauman 2001] (en) Ronald Rivest, Adi Shamir et Yael Tauman, « How to Leak a Secret », Asiacrypt, lNCS, , p. 552−565 (lire en ligne [PDF])
- (en) Rynomster et Tecnovert, « Shadow: Zero-knowledge Anonymous Distributed Electronic Cash via Traceable Ring Signatures » [PDF]
Liens externes
- Pierre-Louis Cayrel, Optimisation des cryptosystèmes basés sur les codes correcteurs d’erreurs (Thèse de Doctorat) (lire en ligne), chap. 6 (« signature de cercle à seuil, présentation de la signature de cercle »).