Roncier (théorie des graphes)
En théorie des graphes, un roncier (ou une ronce) pour un graphe non orienté G est une famille de sous-graphes connexes de G qui sont reliés deux-à-deux : pour chaque paire de sous-graphes disjoints, il existe une arête de G qui a une extrémité dans chacun de ces sous-graphes. L'ordre d'un roncier est la plus petite taille d'une couverture, c'est-à-dire d'un ensemble de sommets de G qui a une intersection non vide avec chacun des sous-graphes. Les ronciers peuvent être utilisés pour caractériser la largeur arborescente de G[1].
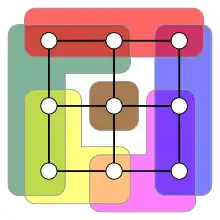
Largeur d'arbre et refuge
Un refuge d'ordre k dans un graphe G est une fonction qui associe, à chaque ensemble X de moins de k sommets, une composante connexe de de telle sorte que deux sous-ensembles et quelconques ont une arête qui les relie. Ainsi, l'ensemble des images de forme un roncier dans G d'ordre k. Réciproquement, chaque roncier peut être utilisé pour déterminer un refuge : pour chaque ensemble X de taille inférieure à l'ordre du roncier, il existe une composante connexe unique qui contient tous les sous-graphes du roncier qui sont disjoints de X.
Comme l'ont montré Seymour et Thomas[1], l'ordre d'un roncier (ou de manière équivalente d'un refuge) caractérise la largeur arborescente : un graphe a un roncier d'ordre k si et seulement s'il a une largeur d'arbre supérieure ou égale à k-1.
Taille des ronciers
Les graphes expanseurs de degré borné ont une largeur arborescente proportionnelle à leur nombre de sommets, et ont donc également des ronciers d'ordre linéaire. Cependant, comme l'ont montré Martin Grohe et Dániel Marx[2], pour ces graphes, un roncier d'un ordre aussi élevé doit contenir un nombre exponentiel d'ensembles. Plus précisément, pour ces graphes, même les ronciers dont l'ordre est légèrement supérieur à la racine carrée de la largeur arborescente doivent avoir une taille exponentielle. Cependant, Grohe et Marx ont également montré que tout graphe de largeur arborescente k admet un roncier de taille polynomiale et d'ordre [2].
Complexité de calcul
Étant donné que les ronciers peuvent avoir une taille exponentielle, il n'est pas toujours possible de les construire en temps polynomial pour des graphes de largeur arborescente non bornée. Cependant, lorsque la largeur arborescente est bornée, une construction en temps polynomial est possible : il est possible de trouver un roncier d'ordre k, quand il existe, en temps , où n est le nombre de sommets du graphe donné. Des algorithmes encore plus rapides existent pour les graphes avec peu de séparateurs minimaux[3].
Bodlaender, Grigoriev et Koster[4] ont étudié des heuristiques pour trouver des ronciers d'ordre élevé. Leurs méthodes ne génèrent pas toujours des ronciers d'ordre proche de la largeur arborescente du graphe d'entrée, mais pour les graphes planaires, elles donnent un taux d'approximation constant. Kreutzer et Tazari[5] donnent des algorithmes randomises qui, sur des graphes de largeur arborescente k, trouvent des ronciers de taille polynomiale et d'ordre en un temps polynomial, approchant ainsi, à un facteur logarithmique près, l'ordre dont Grohe et Marx[2] ont montré l'existence pour les ronciers de taille polynomiale.
Ronciers orientés
La notion de roncier a également été défini epour les graphes orientés[6] - [7]. Dans un graphe orienté D, un roncier est une collection de sous-graphes fortement connexes de D qui sont reliés entre eux deux-à-deux : pour chaque paire d'éléments disjoints X, Y du roncier, il existe dans D un arc de X à Y et un arc de Y à X. L'ordre d'un roncier est la plus petite taille d'un ensemble de représentants, un ensemble de sommets de D qui a une intersection non vide avec chacun des éléments du roncier. Le nombre de ronces de D est l'ordre maximum d'un roncier de D. Le nombre de ronces d'un graphe orienté est, à un facteur constant près, égal à sa largeur arborescente orientée[8].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bramble (graph theory) » (voir la liste des auteurs).
- Paul D. Seymour et Robin Thomas, « Graph Searching and a Min-Max Theorem for Tree-Width », Journal of Combinatorial Theory, Series B, vol. 58, no 1, , p. 22–33 (ISSN 0095-8956, DOI 10.1006/jctb.1993.1027). Les ronciers sont appelés "screens" et leur ordre est appelé "thickness".
- Martin Grohe et Dániel Marx, « On tree width, bramble size, and expansion », Journal of Combinatorial Theory Série B, vol. 99, no 1, , p. 218–228 (DOI 10.1016/j.jctb.2008.06.004, MR 2467827).
- Mathieu Chapelle, Frédéric Mazoit et Ioan Todinca, « Constructing brambles », dans Mathematical Foundations of Computer Science 2009: 34th International Symposium, MFCS 2009, Novy Smokovec, High Tatras, Slovakia, August 24-28, 2009, Proceedings, Berlin, Springer, coll. « Lecture Notes in Computer Science » (no 5734), , 223–234 p. (DOI 10.1007/978-3-642-03816-7_20, Bibcode 2009LNCS.5734..223C, MR 2539494).
- Hans L. Bodlaender, Alexander Grigoriev et Arie M. C. A. Koster, « Treewidth lower bounds with brambles », Algorithmica, vol. 51, no 1, , p. 81–98 (DOI 10.1007/s00453-007-9056-z
 , MR 2385750).
, MR 2385750). - Stephan Kreutzer et Siamak Tazari, « On brambles, grid-like minors, and parameterized intractability of monadic second-order logic », dans Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '10), (lire en ligne), p. 354–364.
- Bruce Reed, « Introducing directed tree width », Elsevier, vol. 3, , p. 222–229 (DOI 10.1016/S1571-0653(05)80061-7)
- Thor Johnson, Neil Robertson, Paul Seymour et Robin Thomas, « Directed Tree-Width », Journal of Combinatorial Theory, Series B, vol. 82, no 1, , p. 138–154 (DOI 10.1006/jctb.2000.2031)
- Ken-ichi Kawarabayashi et Stephan Kreutzer, « The Directed Grid Theorem », ACM, Portland, Oregon, USA, , p. 655–664 (DOI 10.1145/2746539.2746586, arXiv 1411.5681)






