Rêve du deuxième année

En mathématiques, le rêve du deuxième année désigne les deux identités :

{\begin{aligned}\int _{0}^{1}x^{-x}\,\mathrm {d} x&=\sum _{n=1}^{\infty }n^{-n}\approx 1,291285997...\\\int _{0}^{1}x^{x}\,\mathrm {d} x&=\sum _{n=1}^{\infty }(-1)^{n+1}n^{-n}=-\sum _{n=1}^{\infty }(-n)^{-n}\approx 0,783430510...\end{aligned}}

Voir la suite A073009 de l'OEIS et la suite A083648 de l'OEIS.

Elles ont été découvertes en 1697 par Johann Bernoulli.

Le nom « rêve du deuxième année », apparu en 2004[1], fait référence au « rêve du première année » qui est la fausse[alpha 1] identité $(x + y) n = x n + y n$ . À l'inverse, les deux identités du rêve du deuxième année (en anglais sophomore's dream), qui donnent la même impression d'être « trop belles pour être vraies » — en particulier la première — sont vraies.

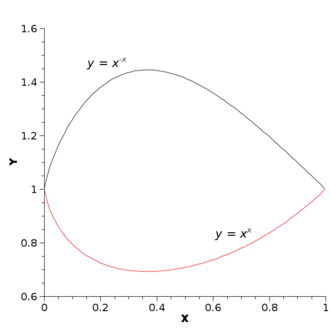
Graphe des fonctions

y = x x

(rouge, en bas) et

y = x - x

(gris, en haut) sur l'intervalle

]0 ; 1]

Historique

Jean Bernoulli a découvert ces égalités en s'intéressant à la différentiation du logarithme naturel.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sophomore's dream » (voir la liste des auteurs).

Notes

Fausse en général, mais correcte dans un anneau commutatif de caractéristique un nombre premier p, si n est une puissance de p, d'après la formule du binôme de Newton.

Références

Borwein et al. (2004), p. 4 et 44.

Voir aussi

Formules

Johann Bernoulli, 1697, collected in Johannis Bernoulli, Opera omnia, vol. 3, p. 376-381
(en) Jonathan Borwein, David H. Bailey et Roland Girgensohn, Experimentation in Mathematics : Computational Paths to Discovery, 2004, 368 p. (ISBN 978-1-56881-136-9)
(en) William Dunham, The Calculus Gallery, Masterpieces from Newton to Lebesgue, Princeton, NJ, Princeton University Press, 2005, 46–51 p. (ISBN 978-0-691-09565-3, lire en ligne), « 3: The Bernoullis (Johann and $x^{x}$ »
Suites A083648 et A073009 de l'OEIS
(en) George Pólya et Gábor Szegő, Problems and Theorems in Analysis, 1998, 393 p. (ISBN 978-3-540-63640-3, lire en ligne), « Part I, problem 160 », p. 36
(en) Eric W. Weisstein, « Sophomore's Dream », sur MathWorld

Fonction

(en) Literature for x^x and Sophomore's Dream, Tetration Forum, 03/02/2010
(en) The Coupled Exponential, Jay A. Fantini et Gilbert C. Kloepfer, 1998
(en) Sophomore's Dream Function, Jean Jacquelin, 2010, 13 pp.
(en) D. H. Lehmer, « Numbers associated with Stirling numbers and x^x », Rocky Mountain Journal of Mathematics, vol. 15,‎ 1985, p. 461 (DOI 10.1216/RMJ-1985-15-2-461)
(en) H. W. Gould (en), « A Set of Polynomials Associated with the Higher Derivatives of y = x^x », Rocky Mountain Journal of Mathematics, vol. 26,‎ 1996, p. 615 (DOI 10.1216/rmjm/1181072076)

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.