Résonance stochastique
La résonance stochastique est l'amélioration des performances d'un dispositif présentant des non-linéarités par l'application d'un signal stochastique (bruit).
La résonance stochastique est le principe de théories
et d'applications dans les domaines
- du traitement du signal,
- de l'audionumérique,
- du traitement graphique digital,
- de la médecine neurologique (stimulation de la perception tactile)
Toutes les applications vérifient cinq conditions :
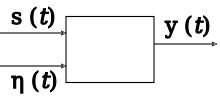
η(t) bruit
y(t) signal traité
- Il existe un signal utile : la variation d'une grandeur s en fonction d'une autre grandeur t transporte une information (t est souvent le temps, mais peut aussi être une autre grandeur).
- Il existe un système ou processus, prenant la grandeur du signal utile en entrée et produisant un signal de sortie.
- On peut créer un bruit dont la valeur en fonction de la grandeur t est aléatoire dans les limites d'une plage de fréquences.
- On peut appliquer le bruit au système en plus de son signal d'entrée.
- Il existe une mesure de performance qui permet d'évaluer l'efficacité du traitement ou l'intégrité de la transmission du système ou processus.
On parle de résonance stochastique quand l'application du bruit au système augmente la performance de celui-ci par rapport au signal.
Théorie en étude du climat
La théorie de la résonance stochastique a été introduite au début des années 1980 pour expliquer la récurrence des ères glaciaires. La survenue d'ères glaciaires résulte d'une interaction non linéaire entre une cause périodique due aux mouvements planétaires (signal cohérent) et une cause aléatoire due aux perturbations atmosphériques et climatiques (bruit). Il apparaît que l'influence sur le résultat de la cause cohérente périodique peut être renforcée en augmentant la cause aléatoire[2].
Usage en traitement du signal
On utilise une technique de résonance stochastique pour
- décorréler l'erreur de quantification,
- transmettre des signaux de niveau inférieur au plus petit échelon de conversion.
Un convertisseur, ou un système de requantification après des calculs avec une résolution supérieure à celle du canal de transmission, présentent une non-linéarité au plus petit échelon de conversion, qui crée une erreur de quantification corrélée au signal, et une non-linéarité.
- erreur de quantification corrélée avec le signal
Si le signal est une sinusoïde d'amplitude du même ordre de grandeur que l'échelon de quantification, l'erreur de quantification est corrélée avec le signal.
- signaux faibles non transmis
La sortie du système est, à chaque échantillon, un nombre entier. La valeur d'entrée peut avoir plusieurs valeurs entre celles qui correspondent à des nombres entiers en sortie. Que l'on tronque les valeurs d'entrée ou qu'on les arrondisse, il existe un niveau l limite de répartition entre chaque valeur de sortie. Soit un signal d'amplitude 0,4 fois l'échelon de conversion : s'il est transmis comme ((l + 0,1), (l + 0,1), (l + 0,5), (l + 0,5), (l + 0,1), (l + 0,1), (l + 0,5), (l + 0,5)), il n'est pas transmis. S'il est transmis comme ((l - 0,1),(l - 0,1), (l + 0,3), (l + 0,3), (l - 0,1),(l - 0,1), (l + 0,3), (l + 0,3)), il se retrouve en sortie avec une amplitude de 1 échelon.
- amélioration par l'ajout de bruit
En ajoutant un bruit d'amplitude égale à un échelon en entrée du système, les signaux faibles apparaissent, statistiquement, bien que de niveau inférieur à celui du bruit. On peut les détecter par un traitement adéquat.
Signal audionumérique
L'ajout de bruit au signal pour effectuer la décorrélation de l'erreur de quantification a été étudiée et mise en pratique dans le courant des années 1980 sous le nom de dithering (tremblement)[3].
Notes et compléments
- Voir une liste d'articles dans le journal de l'académie des Sciences des États-Unis
- Xavier Godivier et François Chapeau-Blondeau, « La résonance stochastique ou la transmission non linéaire du signal favorisée par le bruit », dans Colloque de Recherche Doctorale Automatique, Génie informatique, Image, Signal, Angers, (lire en ligne)
- (en) John Vanderkooy et Stanley Lipshitz, « Dither in digital audio », Journal of the Audio Engineerig Society, vol. 35,
Articles connexes
Bibliographie
- (en) Robert Alexander Wannamaker, The Theory of Dithered Quantization : Ph.D. Thesis presented to the University of Waterloo, Waterloo, Ontario, Canada, L'auteur, , 223 p. (lire en ligne)