Réseau invariant d'échelle

Un réseau invariant d'échelle (ou réseau sans échelle, ou encore scale-free network en anglais) est un réseau dont les degrés suivent une loi de puissance. Plus explicitement, dans un tel réseau, la proportion de nœuds de degré k est proportionnelle à $k^{\boldsymbol {-\gamma }}$ pour $k$ grand, où $\gamma$ est un paramètre (situé entre 2 et 3 pour la plupart des applications).

Beaucoup de réseaux, comme le réseau du web, les réseaux sociaux et les réseaux biologiques semblent se comporter comme des réseaux invariants d'échelle, d'où l'importance de ce modèle.

Définition

Un réseau invariant d'échelle est un réseau dont la proportion de nœuds de degré $k$ , noté $P(k)$ suit la loi :

P(k)\ \sim \ k^{\boldsymbol {-\gamma }}

Le coefficient $\gamma$ , appelé exposant d'invariance d'échelle est strictement positif[1].

Propriétés

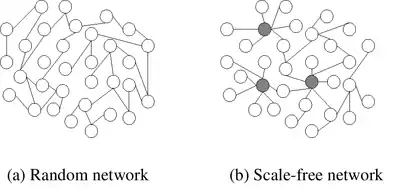
Exemple d'un réseau aléatoire selon le modèle Erdős-Rényi et d'un graphe invariant d'échelle

Exemples de réseaux réels conjecturés invariants d'échelle

De nombreux réseaux ont été décrits comme invariants d'échelle et certains sont présentés ici. Cependant cette caractérisation peut souvent être remise en question, notamment à cause des éléments rares dans la queue de la distribution[2] - [3].

Quelques exemples de réseaux conjecturés invariants d'échelle :

Le réseau des citations dans les articles de recherche scientifique, étudiées par Derek Price, avec le modèle de Price (en)[4].
Le réseau World Wide Web, dont l'étude, par Barabási et Albert[5] a donné naissance au terme scale-free network. Dans ce cas une dichotomie est faite entre les hub qui sont les nœuds les plus reliés, et les autres nœuds.
Les réseaux de collaborations, comme celui des collaborations entre scientifiques (publications communes), entre entreprises, de films communs entre acteurs ou encore de relations sexuelles[6].
Les réseaux biologiques dans les cellules[7].

Modèles de construction

Plusieurs modèles ont été donnés pour expliquer l’émergence des réseaux invariant d'échelle, en particulier le modèle de Barabási-Albert.

Notes et références

La définition peut par exemple être trouvée dans le résumé (Hein, Schwind et König 2006) ou dans l'article original (Barabási et Albert 1999).
Pour plus des détails sur ces remises en question et une liste d'exemples voir (Clauset, Shalizi et Newman 2009).
Erica Klarreich, « Scant Evidence of Power Laws Found in Real-World Networks », sur Quanta magazine, 15 février 2018
Introduit dans (en) D. J. De Solla Price, « Networks of Scientific Papers », Science, vol. 149, n^o 3683,‎ 1965, p. 510-515 (PMID 14325149, DOI 10.1126/science.149.3683.510)
(Barabási et Albert 1999)
Voir chapitre 3.3 de (Dorogovtsev et Mendes 2013).
(en) Réka Albert, « Scale-free networks in cell biology », Journal of Cell Science, vol. 118,‎ novembre 2005, p. 4947-4957 (PMID 16254242, DOI 10.1242/jcs.02714, lire en ligne)

Bibliographie

Albert-László Barabási et Éric Bonabeau, « Les réseaux invariants d'échelle », Pour la Science, n^o 66,‎ janvier 2010 (lire en ligne)

(en) Aaron Clauset, Cosma Rohilla Shalizi et Mark EJ Newman, « Power-law distributions in empirical data », SIAM review, vol. 51, n^o 4,‎ 2009, p. 661-703 (lire en ligne)

(en) Albert-László Barabási et Réka Albert, « Emergence of scaling in random networks », Science, vol. 286,‎ octobre 1999, p. 509-512 (DOI 10.1126/science.286.5439.509, lire en ligne)

(en) Oliver Hein, Michael Schwind et Wolfgang König, « Scale-free networks », Wirtschaftsinformatik, Springer, vol. 48, n^o 4,‎ 2006, p. 267-275 (lire en ligne)

(en) Sergei N Dorogovtsev et José Mendes, Evolution of networks : From biological nets to the Internet and WWW, Oxford University Press, 2013 (lire en ligne)

Voir aussi

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Scale-free network » (voir la liste des auteurs).