Qualité métrologique d'un appareil de mesure

La sensibilité est un paramètre exprimant la variation du signal de sortie d'un appareil de mesure en fonction de la variation du signal d'entrée.

Un appareil est d'autant plus sensible qu'une petite variation de la grandeur G à mesurer provoquera un changement plus grand de l'indication donnée par l'appareil de mesure.

Note : si la valeur d'entrée est de même nature que la valeur de sortie, la sensibilité est appelée gain.

La sensibilité au voisinage d'une valeur donnée de la grandeur G à mesurer s'exprime de la manière suivante :

${\displaystyle S={\frac {{\rm {d}}I}{{\rm {d}}G}}}$ [1]

${\displaystyle I}$ : indication donnée par l'essai

${\displaystyle G}$ : quantité de grandeur à mesurer

On considère généralement qu'il s'agit de la pente de la courbe de graduation sur un intervalle : la sensibilité moyenne.

On peut écrire alors :

${\displaystyle {\bar {S}}={\frac {\Delta I}{\Delta G}}}$ [2]

Exemple : la largeur d'échelon d'un volucompteur est de 1 cm et la valeur de cet échelon est de 5 cl.

${\displaystyle S={\frac {10\;{\rm {mm}}}{5\;{\rm {cl}}}}={\frac {2\;{\rm {mm}}}{\rm {cl}}}}$

La formule [2] n'a de sens que si sur cet intervalle de mesure l'appareil est linéaire, c’est-à-dire si la sortie est proportionnelle à l'entrée.

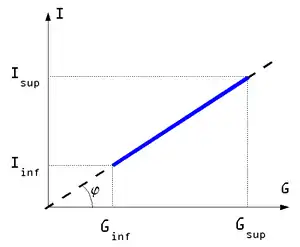
${\displaystyle S={\frac {{\rm {d}}I}{{\rm {d}}G}}=\operatorname {tan} \ \varphi }$ [3] ou encore ${\displaystyle \varphi =\operatorname {Arctan} \left({\frac {{\rm {d}}I}{{\rm {d}}G}}\right)}$

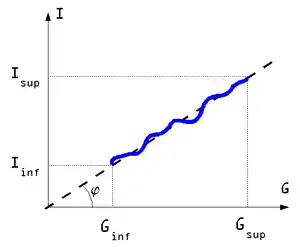
En pratique, on réalise une courbe d'étalonnage où la linéarité est approchée. Pour déterminer la droite on peut utiliser la méthode des moindres carrés.

Il faut préciser que généralement une pente (d'une dépendance linéaire entre deux grandeurs physiques) a sa propre unité de mesure. Prenons comme premier exemple la dépendance entre l'intensité du courant dans un circuit électrique simple (contenant une source de tension continue et une résistance) en fonction de la tension. Dans ce cas la pente de la droite ${\displaystyle I={\frac {U}{R}}}$ a la dimension de l'inverse d'une résistance électrique. Et cette pente est calculée à partir de la formule ${\displaystyle {\frac {\Delta I}{\Delta U}}}$, ou ${\displaystyle {\frac {I}{U}}}$ (point ${\displaystyle U}$,${\displaystyle I}$ pris sur la droite) car la droite doit passer par l'origine du système de coordonnées. Il ne faut pas confondre la pente de la droite physique (ou logique) et la pente de la droite dessinée, qui dépend des échelles utilisées.

Prenons un autre exemple : la détermination de la constante de Planck à partir de l'effet photoélectrique faite par Millikan : en fonction de la fréquence du rayonnement monochromatique qui produit l'effet photoélectrique externe, on détermine la tension électrique de freinage qui arrête les photoélectrons. La loi de conservation de l'énergie pour ce processus s'écrit : ${\displaystyle h\nu =E_{\text{ext}}+eU}$ où ${\displaystyle h}$ est la constante de Planck, ${\displaystyle \nu }$ la fréquence du rayonnement monochromatique, ${\displaystyle E_{\text{ext}}}$ le travail d'extraction (des électrons du matériau), ${\displaystyle e}$ est la charge des électrons et ${\displaystyle U}$ la tension de freinage qui arrête les photoélectrons. La représentation ${\displaystyle U(\nu )}$ c'est-à-dire ${\displaystyle U=-{\frac {E_{\text{ext}}}{e}}+{\frac {h\nu }{e}}}$ donne une droite dont la pente théorique est ${\displaystyle {\frac {h}{e}}}$ ; la pente expérimentale reste obtenue à partir de la droite tracée, par ${\displaystyle {\frac {\Delta U}{\Delta \nu }}}$. Finalement on égale les deux pentes, théorique et expérimentale, on connaît la valeur de la charge de l'électron et on obtient la valeur de la constante de Planck.

Pour des métaux et pour la lumière visible on a des fréquences de l'ordre de 10¹⁴ Hz et des tensions de l'ordre du volt, ce qui donne des pentes physiques de l'ordre de 10⁻¹⁵ V/Hz ou 10⁻¹⁵ V s. La valeur numérique, de 10⁻¹⁵, est proche de zéro, ce qui conduirait faussement à l'idée que l'« angle », si on considère la signification fausse de la pente physique comme la tangente d'un angle sur le graphique, est presque nul. On a omis délibérément l'unité de mesure pour la pente dans ce raisonnement, mais normalement on ne doit jamais le faire. En plus, en ce qui concerne la représentation graphique, les meilleurs résultats expérimentaux sont obtenus quand la pente visuelle est proche de 45°, c'est-à-dire qu'on choisit correctement les échelles verticale et horizontale.

L'erreur de justesse est l'erreur globale résultant de toutes les causes pour chacun des résultats de mesure pris isolément. C'est donc l'aptitude de l'appareil à donner des résultats qui ne sont pas entachés d'erreur.

Dans le cas de mesures multiples c'est l'écart entre le résultat moyen et la valeur vraie.

${\displaystyle J={\bar {v}}-V}$

${\displaystyle {\bar {v}}}$ : moyenne arithmétique d'un grand nombre de mesures

${\displaystyle V}$ : valeur vraie (ou conventionnellement vraie)

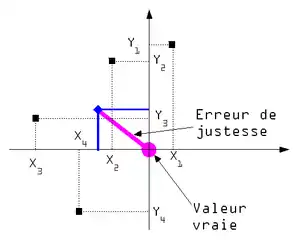
Si l'on effectue une représentation en deux dimensions en considérant la valeur vraie comme l'origine on peut considérer l'erreur de justesse comme la distance ${\displaystyle {\bar {d}}}$ entre le barycentre de l'ensemble des mesures et l'origine.

Représentation dans un espace en deux dimensions de la justesse.

${\displaystyle {\begin{matrix}&{\bar {d}}&=&{\sqrt {{\rm {(\sum \cdot \ ({\frac {Ox_{i}}{n}})^{2})}}+{\rm {(\sum \cdot \ ({\frac {Oy_{i}}{n}})^{2})}}{\rm {}}}}\\&&=&{\sqrt {{\rm {({\overline {Ox}})^{2}}}+{\rm {({\overline {Oy}})^{2}}}}}\end{matrix}}}$

Définition : la fidélité est l'aptitude d'un appareil de mesure à donner des mesures exemptes d'erreurs accidentelles.

La fidélité définit la dispersion des résultats. Si on n'effectue qu'une seule mesure, la fidélité représente la probabilité qu'elle soit représentative du résultat moyen. Ce dernier aurait été obtenu en effectuant une infinité de mesures.

Nota : le résultat moyen est lui-même entaché de l'erreur de justesse.

Si on effectue un ensemble de mesures d'une grandeur G, on obtient une valeur maximum (V_max) et une valeur minimum (V_min). Les erreurs limites de fidélité sont alors :

${\displaystyle F_{\text{max}}=+{\frac {V_{\text{max}}-V_{\text{min}}}{2}}}$

${\displaystyle F_{\text{min}}=-{\frac {V_{\text{max}}-V_{\text{min}}}{2}}}$

Exemple : des mesures répétées à l'aide d'un voltmètre donnent :

${\displaystyle U_{\text{max}}=100,2\;{\rm {V}}}$

${\displaystyle U_{\text{min}}=99,7\;{\rm {V}}}$

${\displaystyle F=\pm {\frac {100,2-99,7}{2}}=\pm {\frac {0,5}{2}}=\pm 0,25\;{\rm {V}}}$

On peut représenter symboliquement la fidélité, la justesse et l'exactitude de la manière suivante :

Représentation symbolique de la fidélité, la justesse et l'exactitude en métrologie.

Dans le premier cas, les mesures sont proches les unes des autres (bonne fidélité) mais en dehors de la zone de probabilité de la valeur vraie (mauvaise justesse).

Dans le deuxième cas, les mesures sont au contraire bien dans la zone où se trouve la valeur vraie et le « barycentre » des points est au centre de la zone rouge (bonne justesse) mais bien que bonnes, les mesures sont dispersées entre elles (mauvaise fidélité).

Le dernier cas présente des mesures justes (dans la zone de la valeur vraie) et fidèles (proches les unes des autres). C'est le cas d'un bon appareil de mesure, à qui l'apport d'une correction n'est a priori pas nécessaire et les mesures effectuées avec l'appareil sont exactes.

• Erreur (métrologie)
• Incertitude de mesure
• Calcul d'incertitude
• Critères de dispersion
• Métrologie
• Étalonnage
• Capabilité d'un moyen de mesure

• Vocabulaire international de métrologie — Concepts fondamentaux et généraux et termes associés (VIM), BIPM.

• ISO 5725-1 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 1 : principes généraux et définitions.
• ISO 5725-2 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 2 : méthode de base pour la détermination de la répétabilité et de la reproductibilité d'une méthode de mesure normalisée.
• ISO 5725-3 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 3 : mesures intermédiaires de la fidélité d'une méthode de mesure normalisée.
• ISO 5725-4 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 4 : méthodes de base pour la détermination de la justesse d'une méthode de mesure normalisée.
• ISO 5725-5 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure - Partie 5 : méthodes alternatives pour la détermination de la fidélité d'une méthode de mesure normalisée.
• ISO 5725-6 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure. Partie 6 : utilisation dans la pratique des valeurs d'exactitude.
• ISO/TR 22971 : Exactitude (justesse et fidélité) des résultats et méthodes de mesure - Lignes directrices pratiques pour l'utilisation de l'ISO 5725-2:1994 pour la conception, la mise en œuvre et l'analyse statistique des résultats de répétabilité et de reproductibilité interlaboratoires.

• Jean-Claude Engrand, De la métrologie fondamentale à son application industrielle, éditeur Librairie scientifique Albert Blanchart, 1976.
• Jean Perdijon, La mesure science et philosophie, coll. « Domino », éditeur Flammarion, 1998 (ISBN 2-08-035580-5) ; Pour faire bonne mesure, EDP sciences, 2020.
• A. Defix, Élément de métrologie générale et de métrologie légale, École nationale supérieure du pétrole et des moteurs, édition Technip, 1985, 2^e éd. (ISBN 2-7108-0496-4).
• Joffin Christiane, Lafont Françoise, Mathieu Élisabeth Je pratique la métrologie, Lexitis Éditions, 2019, 1e edition, 560 p., (ISBN 978-2-3623-3185-5)
• Joffin Christiane, Lafont Françoise, Mathieu Élisabeth (2017) Mesure et Instrumentation. Delagrave-Casteilla, Éditions, 2017, 1e edition, 248 p., (ISBN 978-2-2063-0342-0)