Propriété de relèvement des homotopies

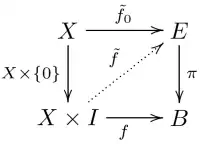
Supposons désormais que toutes les cartes sont des fonctions continues d'un espace topologique à un autre. Étant donné une application ${\displaystyle \pi \colon E\to B}$, et un espace ${\displaystyle X\,}$, on dit que ${\displaystyle (X,\pi )}$ a la propriété de relèvement des homotopies[1] - [2], si:

• pour toute homotopie ${\displaystyle f\colon X\times [0,1]\to B}$, et
• pour n'importe quelle application ${\displaystyle {\tilde {f}}_{0}\colon X\to E}$ relevant ${\displaystyle f_{0}=f|_{X\times \{0\}}}$ (c'est-à-dire que l'on a ${\displaystyle f_{0}=\pi \circ {\tilde {f}}_{0}}$),

il existe une homotopie ${\displaystyle {\tilde {f}}\colon X\times [0,1]\to E}$ relevant ${\displaystyle f\,}$ (c'est-à-dire ${\displaystyle f=\pi \circ {\tilde {f}}}$) qui satisfait également ${\displaystyle {\tilde {f}}_{0}=\left.{\tilde {f}}\right|_{X\times \{0\}}}$.

Le carré extérieur (sans la flèche en pointillé) commute si et seulement si les hypothèses de la propriété de relèvement sont vérifiée. Un relèvement ${\displaystyle {\tilde {f}}}$ correspond à une flèche en pointillé faisant commuter le diagramme.

Si l'application ${\displaystyle \pi \,}$ satisfait la propriété de relèvement des homotopies par rapport à tout espace X, alors ${\displaystyle \pi \,}$ s'appelle une fibration.

Une notion plus faible de fibration est la fibration de Serre, pour laquelle le relèvement d'homotopie n'est requis que pour tous les CW-complexes ${\displaystyle X}$.

Il existe une généralisation commune de la propriété de relèvement des homotopies et de la propriété de prolongement des homotopies. Étant donné une paire d'espaces ${\displaystyle X\supseteq Y}$, on note simplement${\displaystyle T\mathrel {:=} (X\times \{0\})\cup (Y\times [0,1])\subseteq X\times [0,1]}$. Soit de plus une application ${\displaystyle \pi \colon E\to B}$, on dit que ${\displaystyle (X,Y,\pi )}$ a la propriété d'extension de relèvement des homotopies si :

• Pour toute homotopie ${\displaystyle f\colon X\times [0,1]\to B}$, et
• Pour tout relèvement ${\displaystyle {\tilde {g}}\colon T\to E}$ de ${\displaystyle g=f|_{T}}$, il existe une homotopie ${\displaystyle {\tilde {f}}\colon X\times [0,1]\to E}$ qui couvre ${\displaystyle f}$ (i.e. tel que ${\displaystyle \pi {\tilde {f}}=f}$ ) et prolonge ${\displaystyle {\tilde {g}}}$ (i.e. tel que ${\displaystyle \left.{\tilde {f}}\right|_{T}={\tilde {g}}}$ ).

La propriété de relèvement des homotopies de ${\displaystyle (X,\pi )}$ est obtenue en prenant ${\displaystyle Y=\emptyset }$, de sorte que ${\displaystyle T}$ soit simplement ${\displaystyle X\times \{0\}}$.

La propriété d'extension d'homotopie de ${\displaystyle (X,Y)}$ est obtenue en prenant ${\displaystyle \pi }$ constante.

• propriété de prolongement des homotopies
• Fibration

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Homotopy lifting property » (voir la liste des auteurs).

• Norman Steenrod, The Topology of Fibre Bundles, Princeton, Princeton University Press, 1951 (ISBN 0-691-00548-6, lire en ligne )
• Sze-Tsen Hu, Homotopy Theory, New York, Academic Press Inc., 1959, Third Printing, 1965 éd. (ISBN 0-12-358450-7, lire en ligne )
• Dale Husemoller, Fibre Bundles, New York, Springer, 1994, Third éd. (ISBN 978-0-387-94087-8)
• Allen Hatcher, Algebraic Topology, Cambridge, Cambridge University Press, 2002 (ISBN 0-521-79540-0, lire en ligne)
• Jean-Pierre Marquis (2006) "A path to Epistemology of Mathematics: Homotopy theory", pages 239 à 260 dans The Architecture of Modern Mathematics, J. Ferreiros & JJ Gray, éditeurs, Oxford University Press (ISBN 978-0-19-856793-6)

• (en) « Propriété de relèvement des homotopies », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)