Projection cylindrique centrale
La projection cylindrique centrale (ou projection cylindrique perspective[1]) est une projection cartographique correspondant à une projection centrale de la sphère terrestre sur un cylindre tangent à l'équateur effectuée à partir du centre de la terre. Le cylindre est ensuite coupé le long d'un méridien et déroulé pour obtenir une carte plate[2].
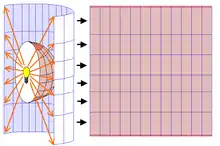
Les déformations augmentent tellement rapidement, dès que l'on s'éloigne de l'équateur, que la projection cylindrique centrale n'est pas utilisée en cartographie. Elle sert seulement à présenter une illustration aisément compréhensible du principe de la projection cylindrique[2] ou pour montrer l'effet des déformations qu'elle induit qui permet de la distinguer de la projection de Mercator[3] dont la méthode de construction est parfois décrite, de manière erronée, comme équivalente à la projection cylindrique centrale[4].
On ne sait pas qui est à l'origine de cette construction mais elle apparait, avec d'autres projections cylindriques, au XIXe siècle et trouve sa place régulièrement dans des livres de cours pour la comparer avec la projection de Mercator[2]. Comme toute projection cylindrique, la construction peut être généralisée en positionnant le cylindre pour qu'il soit tangent à un autre grand cercle de la sphère que l'équateur[2].
On trouve également cette projection dans la photographie panoramique où elle est communément appelée projection cylindrique. Elle permet de présenter un panorama à 360° qui conserve les droites verticales. Contrairement à d'autres projections cylindriques, elle donne une vision perspectivement correcte des grands objets, une caractéristique intéressante dans les scènes architecturales.
Propriétés géométriques
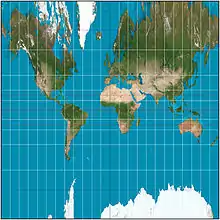
Cette perspective ne permet pas de représenter les pôles, qui sont repoussés à l'infini. En pratique, on arrête souvent la carte aux latitudes voisines de ± 70°. Le canevas des méridiens et des parallèles dessine un quadrillage de droites orthogonales régulièrement espacées en ce qui concerne les méridiens mais dans lequel la distance entre les parallèles augmente quand on s'éloigne de l'équateur. Son indicatrice de Tissot présente des ellipses dont le grand axe est porté par les méridiens et dont la surface augmente à mesure que l'on se rapproche des pôles[3].
Cela fait donc de cette projection une projection[3]
- cylindrique directe
- non conforme (les angles ne sont pas conservés, les cercles sont transformés en ellipses)
- non équivalente (les aires ne sont pas conservées).
Expression mathématique
R représente le rayon du globe générateur ; φ est la latitude ; λ la longitude ; λ₀ est la longitude de référence ; et x et y sont les coordonnées sur la carte.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Central cylindrical projection » (voir la liste des auteurs).
- Yann Ollivier, « Les projections cylindriques »
- Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, Chicago University Press, 1993, pp. 106–107, (ISBN 0-226-76747-7).
- (en) John P. Snyder et Philip M. Voxland, An Album of Map Projections, U.S. Geological Survey, (lire en ligne), p. 30
- World Maps and Globes, Irving Fisher and O. M. Miller, Essential Books, 1944, p. 46.
