Processeur vectoriel
Un processeur vectoriel est un processeur possédant diverses fonctionnalités architecturales lui permettant d'améliorer l’exécution de programmes utilisant massivement des tableaux, des matrices, et qui permet de profiter du parallélisme inhérent à l'usage de ces derniers.

Développé pour des applications scientifiques et exploité par les machines Cray et les supercalculateurs qui lui feront suite, ce type d'architecture a rapidement montré ses avantages pour des applications grand public (on peut citer la manipulation d'images). Elle est implémentée en partie dans les processeurs grand public par des instructions SIMD, soit grâce à une unité de calcul vectoriel dédiée (AltiVec), soit simulée par des instructions bas niveau de type vectoriel (MMX/SSE). Contrairement au SIMD de type MMX, où il faut charger les vecteurs dans les registres en plusieurs opérations puis exécuter une opération supplémentaire sur ses registres, dans une unité vectorielle on charge l'adresse d'une table de vecteurs, la largeur des vecteurs ou du pas et la longueur de la table à traiter par instruction dans un registre, l'instruction vectorielle enchaîne ensuite son calcul sur l'ensemble des vecteurs de cette table.
Jeu d'instruction
Les processeurs vectoriels peuvent être vus comme des processeurs normaux, auxquels on a ajouté un certain nombre d'instructions optimisées pour la gestion des tableaux. Ces instructions optimisées pour les tableaux peuvent être vues comme des variantes d'instructions normales, mais optimisées pour traiter de plus grandes données (pour les accès mémoires), ou capables d'effectuer des opérations en parallèle. Ces instructions sont appelées des instructions vectorielles. Il en existe plusieurs types, qu'on va présenter dans ce qui suit.
Instructions de calcul vectoriel

Les instructions vectorielles sont des instructions qui effectuent plusieurs opérations en parallèle, sur des données différentes. Ces instructions de calcul vectoriel travaillent sur un ensemble de données de même taille et de même type, l'ensemble formant ce qu'on appelle un vecteur. Habituellement, ces vecteurs contiennent plusieurs nombres entiers ou nombres flottants placés les uns à côté des autres. Une instruction de calcul vectoriel va traiter chaque donnée du vecteur en parallèle, à savoir en même temps et indépendamment des autres. Par exemple, une instruction d'addition vectorielle va additionner ensemble les données qui sont à la même place dans deux vecteurs, et placer le résultat dans un autre vecteur, à la même place. Quand on exécute une instruction sur un vecteur, les données présentes dans ce vecteur sont traitées simultanément.
Les opérations en question peuvent être :
- des opérations bit à bit, comme des ET, OU, NOT bitwise ;
- des additions ;
- des soustractions ;
- des multiplications ;
- éventuellement des divisions ;
- ou des opérations mathématiques plus complexes.
Certaines instructions similaires sont disponibles sur certains processeurs non vectoriels. Par exemple, tous les processeurs x86 modernes contiennent des extensions à leur jeu d'instruction, comme le MMX ou le SSE, qui fournissent de telles instructions de calcul vectoriel.
Instructions d'accès mémoire
Tout processeur vectoriel possède des instructions d'accès mémoire diverses, dont au moins une instruction de lecture de vecteurs et une autre pour l'écriture. Sur les anciens processeurs vectoriels, les vecteurs sont lus ou écrits directement en mémoire. Un tel processeur vectoriel est qualifié de mémoire-mémoire. Cette appellation souligne le fait que les vecteurs sont lus et écrits directement dans la mémoire RAM de l'ordinateur, sans stockage intermédiaire visible dans le jeu d'instruction. Mais ce mode de fonctionnement pose quelques problèmes de performances, compte tenu de la lenteur des accès mémoire et de l'inutilité des caches sur ce genre d'architecture. Les processeurs vectoriels de type Load-Store ont été inventés pour résoudre ce problème. Ceux-ci possèdent des registres vectoriels, qui permettent de stocker des vecteurs dans leur intégralité. Un programmeur peut décider de placer certains vecteurs dans ces registres : les résultats intermédiaires de calculs sont enregistrés et accédés depuis ces registres, ce qui est plus rapide que d'aller les enregistrer et les manipuler en mémoire RAM. Pour utiliser ces registres vectoriels efficacement, le processeur doit pouvoir échanger des vecteurs entre la mémoire RAM et ces registres.
Les processeurs vectoriels load-store disposent d'instructions capables de transférer des vecteurs entre la RAM et les registres vectoriels. Ces instructions sont des instructions d'accès mémoire. Sur les processeurs vectoriels, seules ces instructions peuvent aller lire ou écrire en mémoire : toutes les autres instructions vectorielles manipulent des vecteurs placés dans des registres vectoriels. Ces instructions ont des modes d'adressages spécialisés, de par la nature même des vecteurs. Le mode d'adressage principal est le mode d'adressage absolu, à savoir que l'adresse du vecteur manipulé est intégrée directement dans le code machine de l'instruction, mais d'autres modes d'adressage inspirés des modes d'adressages sur architectures non-vectorielles sont aussi disponibles.
Accès mémoires contigus
Avec le mode d'adressage absolu, les instructions peuvent préciser l'adresse mémoire d'un vecteur, qui n'est alors qu'un paquet de données contigües en mémoire. Par exemple, si le processeur manipule des vecteurs de 8 octets, chaque instruction d'accès mémoire utilisant le mode d'adressage absolu va lire ou écrire dans des blocs de 8 octets. L'adresse de départ de ces blocs n'est soumise à aucune contrainte d'alignement, ce qui n'est pas le cas sur les processeurs modernes utilisant des jeux d'instructions comme le SSE, le MMX, etc. La raison à cela est que gérer des accès non alignés en mémoire rend les circuits de lecture/écriture en mémoire plus complexes. En contrepartie, ces contraintes compliquent l'utilisation des instructions vectorielles. Par exemple, un compilateur aura plus de mal à utiliser des instructions de calcul vectorielles en présence de contraintes d'alignement.
Accès en stride et en Scatter-Gather
Sur un processeur vectoriel, d'autres modes de chargements et d'enregistrement des vecteurs sont disponibles. On peut notamment citer l'existence d'accès mémoires en stride et en scatter-gather. Ces accès permettent à une instruction de charger des données dispersées en mémoire pour les rassembler dans un vecteur.
L'accès en stride permet de charger ou d'enregistrer les données d'un vecteur qui sont séparées par un intervalle régulier d'adresses. Une instruction d'accès mémoire voulant utiliser ce mode d'accès a besoin de connaitre l'adresse initiale, celle du premier élément du vecteur, et la distance entre deux données en mémoire. Ce mode d'accès permet aux instructions de mieux gérer les tableaux de structures, ainsi que les tableaux multi-dimensionnels. Lorsqu'on utilise de tels tableaux, il arrive aussi assez souvent que l'on n'accède qu'à certains éléments tous séparés par une même distance. Par exemple, si on fait des calculs de géométrie dans l'espace, on peut très bien ne vouloir traiter que les coordonnées sur l'axe des x, sans accès sur l'axe des y ou des z. Les instructions d'accès mémoire en stride permettent au processeur de gérer de tels cas efficacement.
Dernier type d'accès : le Scatter-Gather. Cet accès sert à mieux gérer les matrices creuses. Dans ces matrices, une grande partie des éléments sont nuls. Dans un souci d'optimisation, seuls les éléments non nuls de la matrice sont stockés en mémoire. Avec ce genre d'organisation, les instructions vectorielles ne seraient pas utilisables sur ce genre de matrices, sans Scatter-Gather. Les accès en Scatter-Gather peuvent être vus comme une généralisation de l'adressage indirect à registre aux vecteurs. Avec cet accès, les adresses de chaque élément du vecteur sont stockées dans un registre vectoriel. L'accès en Scatter-Gather va permettre d'aller lire ou écrire aux diverses adresses rassemblées dans ce vecteur.
Registres des processeurs vectoriels
Comme décrit plus haut, sur certains processeurs, les vecteurs sont stockés dans des registres vectoriels pour plus d’efficacité. Ces registres ont tous une taille fixe. Ces registres ont une taille qui varie entre 64 et 256 bits, pour les tailles les plus courantes.
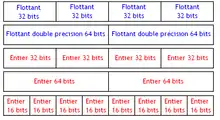
Généralement, ces registres ne sont pas spécialisés : ils peuvent stocker indifféremment des entiers et des flottants. Et leur contenu s’adapte suivant leur taille. C'est-à-dire qu'un registre de 128 bits pourra stocker indifféremment :
- 8 entiers 16 bits ;
- 8 flottants 16 bits ;
- 4 entiers de 32 bits ;
- 4 flottants de 32 bits ;
- 2 entiers de 64 bits ;
- 2 flottants de 64 bits ;
- etc.
Un processeur vectoriel peut aussi incorporer d'autres registres pour faciliter le traitement des diverses instructions. Ces registres vont permettre au compilateur de mieux utiliser les instructions vectorielles pour compiler certaines structures logicielles. Parmi ces registres, on peut citer le Vector Length Register, et le Vector Mask Register.
Vectorisation
L'utilisation des instructions vectorielles permet de faciliter certains traitements sur les tableaux. De nos jours, ces instructions sont difficilement utilisables dans des langages de haut niveau, et c'est au compilateur de traduire certains traitements sur les tableaux en instructions vectorielles. Ces transformations permettant de traduire des morceaux de programmes en instructions vectorielles s'appelle la vectorisation.
Déroulage de boucles
La transformation la plus basique est ce qu'on appelle le déroulage de boucles. Il s'agit d'une optimisation qui vise à réduire le nombre d'itérations d'une boucle en dupliquant son corps en plusieurs exemplaires. Elle est utilisée pour réduire le cout d’exécution des branchements et des autres opérations de comparaison de la boucle. Sur les processeurs SIMD, elle peut s'utiliser afin de réduire le temps d’exécution de boucles qui agissent sur des tableaux. D'ordinaire, les programmeurs utilisent une boucle pour répéter un traitement sur tous les éléments d'un tableau, la boucle traitant un élément à la fois. Nos instructions vectorielles permettent de traiter plusieurs éléments à la fois, ce qui fait que plusieurs tours de boucles peuvent être rassemblés en une seule instruction SIMD. Mais cela ne fonctionne que si les éléments du tableau sont traités indépendamment, ou d'une façon assez simple, auquel cas la boucle peut être vectorisée. Pour cela, le compilateur va répliquer le corps de la boucle (les instructions à répéter) en plusieurs exemplaires dans cette boucle.
Exemple, prenons cette boucle, écrite dans le langage C :
int i;
for (i = 0; i < 100; ++i)
{
a[i] = b[i] * 7 ;
}
Celle-ci peut être déroulée comme suit :
int i;
for (i = 0; i < 100; i+=4)
{
a[i] = b[i] * 7 ;
a[i+1] = b[i+1] * 7 ;
a[i+2] = b[i+2] * 7 ;
a[i+3] = b[i+3] * 7 ;
}
Si le compilateur réplique ces instructions en autant de fois qu'une instruction peut traiter d’éléments simultanément, vectoriser la boucle devient trivial. Dans notre exemple, si jamais le processeur dispose d'une instruction de multiplication capable de traiter 4 éléments du tableau a ou b en une seule fois, la boucle déroulée peut être vectorisée assez simplement.
Strip mining
Le déroulage de boucles n'est toutefois pas une optimisation qui est valable pour toutes les boucles. Reprenons l'exemple de la boucle vue plus haut. Si jamais le tableau à manipuler a un nombre d’éléments qui n'est pas multiple de 4, la boucle ne pourra pas être vectorisée, les instructions de multiplication ne pouvant traiter que 4 éléments à la fois. Pour ce faire, les compilateurs utilisent généralement deux boucles : une qui traite les éléments du tableau avec des instructions SIMD, et une autre qui traite les éléments restants avec des instructions non vectorielles. Cette transformation s'appelle le strip-mining.
Par exemple, si on veut parcourir un tableau de taille fixe contenant 102 éléments, la boucle devra être décrite comme ceci :
int i;
for (i = 0; i < 100; i+=4)
{
a[i] = b[i] * 7 ;
a[i+1] = b[i+1] * 7 ;
a[i+2] = b[i+2] * 7 ;
a[i+3] = b[i+3] * 7 ;
}
for (i = 100; i < 102; ++i)
{
a[i] = b[i] * 7 ;
}
Mais les processeurs vectoriels contiennent des registres pour faciliter le traitement de ce genre de situation. Ils contiennent notamment un Vector Length Register, qui stocke le nombre d’éléments que notre instruction doit traiter. Avec ce registre, il est possible de demander à nos instructions vectorielles de ne traiter que les n premiers éléments d'un vecteur : il suffit de placer la valeur n dans ce registre. Évidemment, n doit être inférieur ou égal au nombre d’éléments maximal du vecteur. Avec ce registre, on n'a pas besoin d'une seconde boucle pour traiter les éléments restants, et une simple instruction vectorielle peut suffire.
Branchements

Autre obstacle à la vectorisation : la présence de branchements conditionnels dans les boucles à vectoriser. Si une boucle contient des branchements conditionnels, il se peut que certaines instructions doivent être appliquées à certains éléments et pas à d'autres. Pour permettre aux compilateurs de dérouler ces boucles contenant des branchements, les processeurs vectoriels incorporent des techniques dans leur jeu d’instructions.
On peut notamment citer le Vector Mask Register, qui permet d'implémenter la prédiction de certaines instructions vectorielles. Celui-ci permet de stocker des informations qui permettront de sélectionner certaines données et pas d'autres pour faire le calcul. Ce Vector Mask Register va stocker un bit pour chaque élément du vecteur à traiter. Si ce bit est à 1, l'instruction doit s’exécuter sur la donnée associée à ce bit. Sinon, l'instruction ne doit pas la modifier. On peut ainsi traiter seulement une partie des registres stockant des vecteurs SIMD.
Micro-architecture
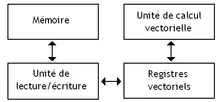
Un processeur vectoriel est composé de plusieurs éléments. Comme tous les processeurs, il contient notamment des registres, des unités de calcul, un séquenceur, et d'autres circuits pour accéder à la mémoire. Tout processeur normal contient des registres et des unités de calcul qui travaillent sur des nombres normaux. Un processeur vectoriel en possède aussi.
Toutefois, un processeur vectoriel va posséder des circuits en plus. Il faut notamment des registres vectoriels, comme vu plus haut. Mais un processeur vectoriel dispose aussi d'une ou de plusieurs unité(s) de calcul spécialisées dans le traitement des vecteurs. De plus, le processeur vectoriel contient aussi un circuit chargé de gérer les échanges de données entre mémoire et registres vectoriels : c'est ce circuit qui gère les instructions d'accès mémoire.
Caches
Les processeurs vectoriels peuvent disposer de mémoires caches. Des mémoires caches d'instruction sont assez courantes. Par contre, les mémoires caches de données sont souvent plus rares sur ce genre de processeur. Cela vient-il du fait que la localité temporelle des programmes utilisant des tableaux est faible ? De plus, les registres vectoriels sont souvent plus longs que les lignes de mémoire cache. Dans ces conditions, passer par une mémoire cache intermédiaire est inutile : autant passer directement par les registres vectoriels. Ainsi, les processeurs vectoriels disposent rarement de mémoires caches, et s'ils en utilisent, celles-ci sont spéciales (elles peuvent gérer un grand nombre de cache mis en attente simultanément).
Qui plus est, sur les processeurs vectoriels disposant de mémoires caches, ces mémoires caches sont souvent utilisées uniquement pour les échanges de données entre mémoire et registres non vectoriels. Les autres échanges ne passent pas par le cache.
Accès mémoires
Comme vu plus haut, les processeurs vectoriels ont besoin de charger ou d'enregistrer des vecteurs complets en mémoire. Nos processeurs ont donc besoin d'une mémoire qui possède un débit binaire assez élevé. Pour cela, un processeur vectoriel est souvent relié à une mémoire composée de plusieurs bancs mémoire.
Chacun de ces bancs mémoire peut être vu comme une sorte de sous-mémoire. Chacun de ces bancs mémoires peut être accédé en parallèle des autres. Ainsi, une lecture ou écriture de vecteur peut être décomposée en plusieurs lectures/écritures, réparties sur plusieurs bancs. Ce qui est plus rapide que d’accéder à une seule mémoire en série.
Pour que cette technique fonctionne, les adresses utilisées par notre programme doivent être réparties sur les différents bancs d'une certaine façon. Il faut que des adresses proches les unes des autres soient réparties dans des bancs différents. Dans le cas le plus simple, des adresses consécutives correspondront à des bancs consécutifs. Ainsi, si je dispose de N bancs, l'adresse A sera placée dans le banc 1, l'adresse A + 1 dans le banc 2… et l'adresse A + N dans le banc N. Une mémoire organisée comme ceci s'appelle une mémoire "interleaved" (entrelacée). Ces mémoires gèrent mal les accès en stride, aussi des organisations plus complexes sont souvent utilisées.
Unité de calcul vectorielle
Contrairement aux processeurs scalaires, les processeurs vectoriels sont spécialement conçus et optimisés pour exécuter la même instruction sur chacune des données contenues dans un tableau. Ils sont surtout utilisés pour le calcul intensif sur supercalculateur.
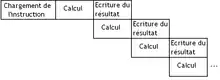
L’exécution d'une opération par l'unité de calcul est pipelinée. Par pipelinée, on veut dire que l’exécution de chaque instruction sera découpée en plusieurs étapes, indépendantes les unes des autres. Cela ressemble un peu au fonctionnement d'une chaîne de montage, dans laquelle on découpe la fabrication d'un objet en plein de sous-étapes qu'on effectue les unes après les autres dans des boxes différents.
Au lieu d'attendre que l’exécution d'une opération sur une donnée soit terminée avant de passer à la suivante, on peut ainsi commencer le traitement d'une nouvelle donnée sans avoir à attendre que l'ancienne soit terminée. Cela permet ainsi d’exécuter plusieurs instructions simultanément dans notre unité de calcul. Toutes ces instructions en cours de calcul sont alors dans des étapes différentes.
Quand une instruction de calcul vectorielle est effectuée par l'unité de calcul, celle-ci exécutera son opération sur chaque élément des vecteurs à traiter. Ces éléments commenceront leur exécution uns par uns, et verront leurs traitement se faire étape par étape.
Startup Time
Avec une unité de calcul pipelinée, il est possible d’exécuter un grand nombre d'opérations simultanées. Si une unité de calcul vectorielle est découpée en N étages (N étapes), alors elle peut gérer N opérations simultanées, chacune dans une étape différente.
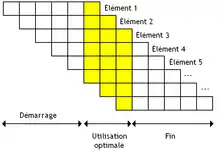
Mais ce nombre maximal d'opérations met un certain temps avant d'être atteint. Il faut que suffisamment d’élément aient été chargés dans le pipeline. Tous les étages sont utilisés avec N éléments chargés dans le pipeline. Chacun de ces éléments étant chargé dans le pipeline un par un, l’utilisation optimale du pipeline n'est atteinte que lorsque l'unité de calcul commence à traiter le N-ème élément de nos vecteurs.
Le même phénomène arrive vers la fin du traitement des vecteurs : ceux-ci n'ont plus assez d’éléments pour remplir les différents étages du pipeline : quand il reste moins d'éléments à traiter qu'il n'y a d'étages, l'utilisation du pipeline est alors sous-optimale.
Chaining
Cette technique du pipeline peut encore être améliorée dans certains cas particuliers. Imaginons que l'on ait trois vecteurs : A, B et C. Pour chaque élément i de ces vecteurs, supposons que l'on souhaite effectuer le calcul Ai + ( Bi * Ci ). Le processeur ne disposant pas d'instruction permettant de faire en une fois ce calcul, le programmeur doit utiliser deux instructions vectorielles : une d'addition, et une autre de multiplication. On pourrait penser que l'on doit effectuer d'abord la multiplication des paquets B et C, stocker le résultat dans un paquet temporaire et effectuer l'addition de ce tableau avec le paquet A.
Mais certains processeurs incorporent des optimisations qui permettent d'utiliser leur pipeline plus efficacement. Le processeur peut en effet fusionner ces deux instructions indépendantes et les traiter en interne comme s'il s’agissait d'une instruction unique. Au lieu d'effectuer la multiplication, puis l'addition séparément pour chaque élément du vecteur, il peut effectuer la multiplication et l'addition pour le premier élément, puis continuer avec le second, etc. En gros, il fusionne plusieurs instructions vectorielles en une seule instruction vectorielle qui regroupe les deux. Ce principe est appelé le Vector Chaining.
Dans un processeur vectoriel implémentant le Vector Chaining, les deux calculs fusionnés sont exécutés l'un après l’autre pour chaque élément. Le pipeline de l'unité de calcul doit être conçu de façon que le résultat de chaque étape d'un calcul soit réutilisable au cycle d’horloge suivant. Ce résultat ne doit pas être enregistré dans un registre vectoriel avant d'être réutilisable.
Marques et modèles
Ces marques fabriquent, ou bien ont fabriqué, des ordinateurs basés sur, ou contenant, des processeurs vectoriels :
- Cray depuis le Cray 1
- NEC gamme SX
- Fujitsu, VP400, VP2000, VPP500
- Hitachi, S-820
- IBM, option vectorielle (VF, pour Vector Facility) du modèle 3090 dénommé 3090/VF
- RISC-V (extension V)
- DEC, processeur vectoriel optionnel sur le modèle 9000 dénommé 9000/440VP
- CDC STAR 100, ETA 10E, Cyber 205, Cyber 2000V
- Texas Instruments TI-ASC (Advanced Scientific Computer)
Certaines consoles de jeu sont équipées de processeurs vectoriels, comme le processeur vectoriel Cell conçu par IBM, Sony et Toshiba pour la PlayStation 3.
Ne sont pas des processeurs vectoriels mais des SIMD :
- AltiVec, le SIMD d'IBM et Motorola, utilisés sur différents processeurs PowerPC, dont les gammes G4 et G5 utilisés notamment sur des ordinateurs Apple dans les années 1990.
- Les différentes extensions SIMD des processeurs x86.
- L‘Emotion Engine, conçu par Sony et Toshiba pour la playStation 2 comporte deux unités appelé VPU, mais qui fonctionnent comme des SIMD.
- NEON, le SIMD d'ARM.