Problème des souris

En mathématiques le problème des souris (ou des trois ou quatre chiens) est un problème de poursuite et d'interception dans lequel on recherche le parcours et le point de rencontre de souris, placées initialement aux coins d'un polygone régulier, qui se poursuivent.

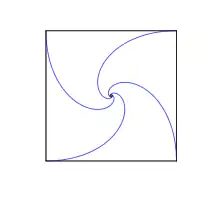
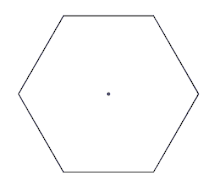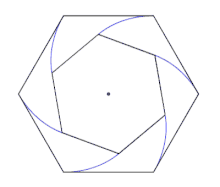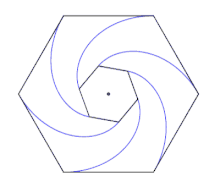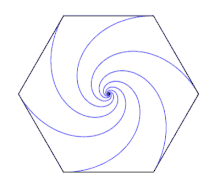
On suppose quatre souris au sommet d'un carré unitaire ABCD. La souris A poursuit la souris B qui poursuit la souris C qui poursuit la souris D qui poursuit la souris A. Les quatre souris se déplacent à la même vitesse constante unitaire. Au fur et à mesure des déplacements les souris parcourent des segments de droites et modifient leur trajectoire pour rester en direction de leur cible. Les souris se rencontrent après un temps d'une unité car la distance entre deux souris voisines décroît toujours à la vitesse d'une unité.

Plus généralement, pour un polygone régulier de n côtés, la distance entre deux souris voisines diminue à la vitesse de ${\displaystyle 1-\cos \left({\frac {2\pi }{n}}\right)}$, elles se rencontrent donc à un temps de ${\displaystyle {\frac {1}{1-\cos \left({\frac {2\pi }{n}}\right)}}}$[1] - [2].

Pour tous les polygones réguliers les souris tracent une spirale logarithmique dont le centre est celui du polygone[3].

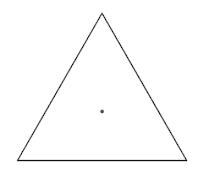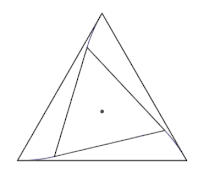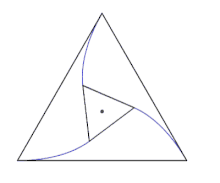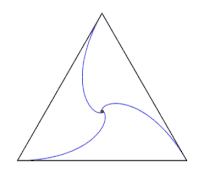
Dans un triangle quelconque, avec des vitesses déterminées de sorte que le triangle déterminé par les souris reste semblable à lui-même, le point de rencontre est l'un des deux points de Brocard du triangle de départ [4] - [5]. Contrairement à ce qui a été parfois écrit [6], ce résultat est faux en général lorsque les trois vitesses sont égales[7].

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.