Potentiel de simple couche

Le potentiel de simple couche est le potentiel de pesanteur créé par une distribution surfacique de masse infiniment mince. Il peut s'écrire au point potentié $P$ comme $V(P)=G\int _{\partial B}r^{-1}\varkappa (Q)\mathrm {d} \sigma (Q)$ , où $Q$ est un point de la surface de masse $\partial B$ , $\varkappa (Q)$ la densité de masse en ce point, et $r$ la distance entre les points $P$ et $Q$ . Le potentiel de simple couche et toutes ses dérivées sont continus dans les volumes intérieurs et extérieurs délimités par la surface, tandis que les dérivées sont discontinues lors du passage au travers de la surface $\partial B$ .

Définition

Contexte : élément volumique ou ponctuel

Le plus souvent on conçoit la force gravifique par unité de masse, appelée gravité, comme engendrée par une distribution volumique de masse donnant lieu à un potentiel newtonien

\displaystyle V(P)=G\int _{B}r^{-1}\rho (Q)\mathrm {d} \tau

où $r$ représente la distance entre un point potentiant $Q$ et un point potentié $P$ et où

\rho (Q)={\frac {\mathrm {d} M(Q)}{\mathrm {d} \tau (Q)}}

désigne la masse volumique (ou densité) du point massique potentiant, autrement dit la limite du rapport de l'élément de masse $\mathrm {d} M$ associé au point massique en $Q$ à l'élément de volume $\mathrm {d} \tau$ associé au même point lorsque $\mathrm {d} \tau$ devient infiniment petit.

Cas surfacique

Il existe de nombreuses situations où l'on est obligé de considérer des distributions de masse non plus volumiques, mais surfaciques ou éventuellement linéaires.

Potentiel de simple couche

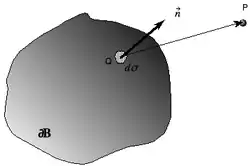
Considérons donc maintenant le potentiel gravifique causé par une distribution surfacique de masse, autrement dit le potentiel d'une surface matérielle $\partial B$ infiniment mince sur laquelle on définit une densité surfacique

\varkappa (Q)={\frac {\mathrm {d} M(Q)}{\mathrm {d} \sigma (Q)}}

Ici, $Q$ désigne un point quelconque appartenant à la surface $\partial B$ , $\mathrm {d} M(Q)$ est l'élément de masse au point potentiant $Q$ , et $\mathrm {d} \sigma (Q)$ est l'élément de surface en $Q$ . Le potentiel en $P$ de cette surface matérielle, appelé potentiel de simple couche, est fourni par

V_{1L}(P)=G\int _{\partial B}r^{-1}\varkappa (Q)\mathrm {d} \sigma (Q)

;

où $r$ est la distance $d(P,Q)$ entre un point potentiant $Q$ et un point potentié $P$ .

Propriétés

On montre que sur la surface $\partial B$ la fonction $V_{1L}$ est continue, mais que ses dérivées premières sont discontinues. En fait, les dérivées tangentielles, c'est-à-dire les dérivées prises dans le plan tangent à la surface au point-frontière considéré, restent continues, mais les dérivées normales diffèrent selon que l'on s'approche de la frontière de l'intérieur ou de l'extérieur. Dans le cas d'une approche de l'extérieur, nous trouvons pour la dérivée normale en $P$ de $V_{1L}$ sur $\partial B$ la limite

\left({\frac {\partial V_{1L}(P)}{\partial n}}\right)_{\text{ext}}=-2\pi G\,\varkappa (P)+G\int _{\partial B}\varkappa (Q){\frac {\partial r^{-1}}{\partial n}}\mathrm {d} \sigma (Q)

Par contre, dans le cas d'une approche de l'intérieur, on a

\left({\frac {\partial V_{1L}(P)}{\partial n}}\right)_{\text{int}}=+2\pi G\,\varkappa (P)+G\int _{\partial B}\varkappa (Q){\frac {\partial r^{-1}}{\partial n}}\mathrm {d} \sigma (Q)

L'opérateur ${\tfrac {\partial }{\partial n}}$ désigne une dérivation dans la direction de la normale extérieure ${\vec {n}}$ .

Nous remarquons ainsi que la dérivée normale ${\tfrac {\partial V_{1L}}{\partial n}}$ du potentiel de simple couche $V_{1L}$ présente une discontinuité au travers de la surface $\partial B$ :

\left({\frac {\partial V_{1L}(P)}{\partial n}}\right)_{\text{ext}}-\left({\frac {\partial V_{1L}(P)}{\partial n}}\right)_{\text{int}}=-4\pi G\,\varkappa (P)

On peut généraliser les relations plus haut pour la dérivée de $V_{1L}$ dans une direction arbitraire ${\vec {m}}$ en tenant compte de la continuité des dérivées tangentielles. Ces expressions généralisées sont les suivantes :

\left({\frac {\partial V_{1L}(P)}{\partial m}}\right)_{\text{ext}}=-2\pi G\,\varkappa (P){\vec {m}}\cdot {\vec {n}}+G\int _{\partial B}\varkappa (Q){\frac {\partial r^{-1}}{\partial m}}\mathrm {d} \sigma (Q)

\left({\frac {\partial V_{1L}(P)}{\partial m}}\right)_{\text{int}}=+2\pi G\,\varkappa (P){\vec {m}}\cdot {\vec {n}}+G\int _{\partial B}\varkappa (Q){\frac {\partial r^{-1}}{\partial m}}\mathrm {d} \sigma (Q)

Les vecteurs ${\vec {m}}$ et ${\vec {n}}$ étant unitaires, le produit scalaire ${\vec {m}}\cdot {\vec {n}}$ représente le cosinus de l'angle fait par les directions ${\vec {m}}$ et ${\vec {n}}$ .

Des discontinuités se produisent seulement lors du passage au travers de la surface matérielle $\partial B$ . Dans les volumes intérieur et extérieur délimités par cette surface, le potentiel de simple couche $V_{1L}$ est partout continu en même temps que toutes ses dérivées. Excepté sur $\partial B$ , il s'obtient comme solution de l'équation de Laplace

\nabla ^{2}\;V_{1L}=0

A l'infini $V_{1L}$ se comporte de la même manière que le potentiel gravifique $V$ d'une distribution de masse volumique. Il tend donc vers zéro comme $r^{-1}$ lorsque $r$ tend vers 0.

Bibliographie

W.A. Heiskanen et H. Moritz, Physical Geodesy, W.H. Freeman and Company, 1967, San Francisco and London. ix + 364 pp.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.