Polynôme osculateur
En analyse, un polynôme osculateur ou osculatoire est un polynôme fournissant une « bonne approximation » d'une fonction.
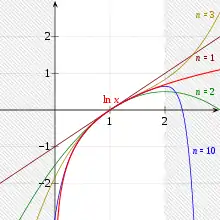
Approximations polynomiales du logarithme népérien en 1 de degrés 1, 2, 3 et 10.
.svg.png.webp)
Approximations polynomiales de la fonction sinus en 0 de degrés 1, 3, 5 et 7.
Définition
Considérons ƒ une fonction réelle n fois dérivable en un point x0. Le polynôme p est dit osculatoire si
En particulier, pour n = 2, on constate donc que le polynôme est tangent et a la même courbure que ƒ en x0.
Formule
Le polynôme osculateur de degré minimal est donc son polynôme de Taylor :
Cependant, pour tout polynôme Q, tout polynôme de la forme
est également osculateur.
Applications
Un polynôme osculateur peut remplacer localement une fonction ƒ. Cela permet d'avoir une fonction plus facile à manipuler.
Voir aussi
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.


