Polynôme de Gegenbauer

Orthogonalité

Les polynômes de Gegenbauer sont orthogonaux sur [-1 ; 1] pour le poids w(x) = (1–x²)^α–1/2 :

${\displaystyle \int _{-1}^{1}C_{n}^{(\alpha )}(x)C_{m}^{(\alpha )}(x)(1-x^{2})^{\alpha -{\frac {1}{2}}}\mathrm {d} x=\delta _{n,m}{\frac {\pi 2^{1-2\alpha }\Gamma (n+2\alpha )}{n!(n+\alpha )\Gamma (\alpha )^{2}}}}$

Récurrence

Les polynômes de Gegenbauer peuvent être construits par la relation de récurrence :

${\displaystyle C_{0}^{(\alpha )}(x)=1,\ C_{1}^{(\alpha )}(x)=2\alpha x,\ C_{n}^{(\alpha )}(x)={\frac {1}{n}}\left(2x(n+\alpha -1)C_{n-1}^{(\alpha )}(x)-(n+2\alpha -2)C_{n-2}^{(\alpha )}(x)\right)}$

Liens avec d'autres suites de polynômes orthogonaux

Les polynômes de Gegenbauer sont solutions de l'équation différentielle :

${\displaystyle (1-x^{2})y''-(2\alpha +1)xy'+n(n+2\alpha )y=0.\,}$

On peut alors remarquer que pour α = 1/2, l'équation se ramène à celle satisfaite par les polynômes de Legendre, et pour α = 1, on retrouve celle des polynômes de Tchebychev de seconde espèce.

• 
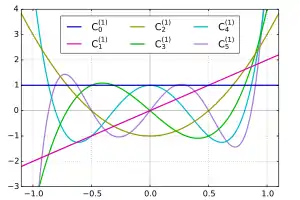  Polynôme de Gegenbauer C(1)
  n(x)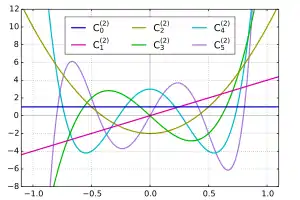
• 
  Polynôme de Gegenbauer C(2)
  n(x)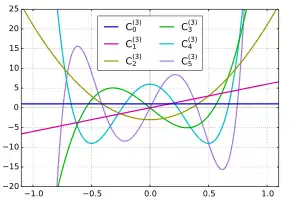
• 
  Polynôme de Gegenbauer C(3)
  n(x)

Les polynômes de Gegenbauer apparaissent comme des prolongements des polynômes de Legendre dans la théorie du potentiel pour les dimensions supérieures à 1.

(en) Eric W. Weisstein, « Gegenbauer Polynomial », sur MathWorld