Polyhex
En mathématiques récréatives, un polyhex est un polyforme avec un hexagone régulier (ou 'hex' pour faire court) comme forme de base.
Énumération
Comme les polyominos, les polyhexs peuvent être dénombrés sous forme de polyhexs libres (où les rotations et les réflexions ont la même forme), les polyhexs fixes (où différentes orientations sont distinctes) et les polyhexs unilatéraux (où les images miroir comptent comme distinctes mais les rotations comptent comme identiques). Ils peuvent également être distingués selon s'ils contiennent des trous ou pas. Le nombre de polyhex pour n = 1, 2, 3, ... hexagones est donné dans l'Encyclopédie en ligne des suites de nombres entiers sous forme de codes OEIS[1] - [2].
| n | Libres OEIS A000228 | Libres avec trous OEIS A038144 | Libres sans trous OEIS A018190 | Unilatéraux OEIS A006535 | Fixes OEIS A001207 |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 3 |
| 3 | 3 | 0 | 3 | 3 | 11 |
| 4 | 7 | 0 | 7 | 10 | 44 |
| 5 | 22 | 0 | 22 | 33 | 186 |
| 6 | 82 | 1 | 81 | 147 | 814 |
| 7 | 333 | 2 | 331 | 620 | 3652 |
| 8 | 1448 | 13 | 1435 | 2821 | 16689 |
| 9 | 6572 | 67 | 6505 | 12942 | 77359 |
| 10 | 30490 | 404 | 30086 | 60639 | 362671 |
Pavage
Tous les polyhexs ayant moins de cinq hexagones peuvent former au moins un pavage plan régulier. De plus, les pavages plans du dihex et des polyhex droits sont invariants par rotation et par réflexion de 180 degrés parallèles ou perpendiculaires au grand axe du dihex (ordre 2 en rotation et ordre 4 en réflexion), et le pavage hexagonal et quelques autres polyhexs (comme l'hexahex avec un trou, ci-dessous) sont invariants sous 60, 120 ou 180° de rotation (ordre 6 en rotation et en réflexion).
| Le monohex | |
| Le dihex | |
| Les 3 trihexes | |
| Les 7 tetrahexes | 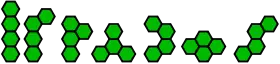 |
| Les 22 pentahexes |  |
| Les 82 hexahexes dont un a un trou | 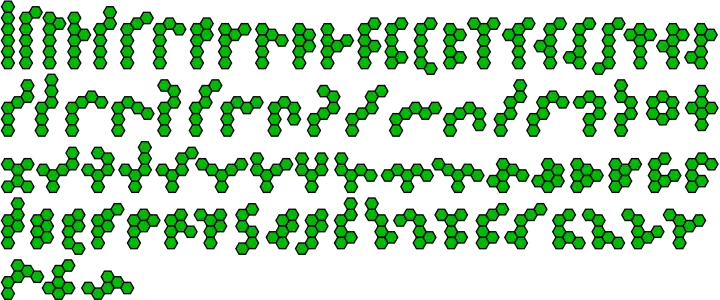 |
Voir aussi
- Hydrocarbure aromatique polycyclique - hydrocarbures dont la structure est à base de polyhexes
Références
- Wolfram Mathworld: Polyhex
- Glenn C. Rhoads, Planar tilings by polyominoes, polyhexes, and polyiamonds, Journal of Computational and Applied Mathematics 174 (2005), No. 2, pp 329–353