Pocket Cube
Le Pocket Cube est un équivalent 2×2×2 du Rubik's cube. Il est constitué de seulement 8 petits cubes (au lieu de 26 pour le Rubik's Cube).
casse-tête
.gif)
| Mécanisme | Rubik's Cube |
|---|---|
| Joueur(s) | 1 |
| Durée annoncée | variable |
| habileté physique | réflexion décision | générateur de hasard | info. compl. et parfaite |
Les états
Orientation le Cube
Prenons un Pocket standard avec ces 6 couleurs ainsi:
(b)lanc , (j)aune , (v)ert , (k)lein , (o)range et (r)ouge.
On pose le Cube sur la table, il possède alors 6 faces ainsi nommées:
(H)aut, (B)as, (A)vant, (P)ostérieur, (G)auche, (D)roite.
On commence par fixer le Cube c'est-à-dire orienter le Cube ainsi :
(H)aut=(b)lanc, (B)as=(j)aune, (A)vant=(v)ert, (P)ostérieur=(k)lein, (G)auche=(o)range, (D)roite=(r)ouge.
Définition un état du Cube
Un état est une configuration des autocollants promenant des rotations de base { H,B,A,P,G,D } ayant respecter l'orientation du Cube. Autrement dit on obtient un état en mélangeant le Cube avec les rotations de base {H,B,A,P,G,D} sans tourner, ni bouger le Cube, c'est comme si le Cube est fixé par un mécanisme et on peut seulement tourner les faces.
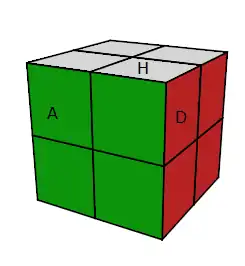 état e
état e
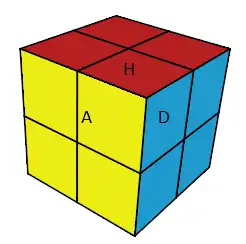 état b
état b
Ex des états :
e = (H=b,A=v) , b=(H=r,A=j) ,....
l'état e se nomme l'état résolu (il y a un seul état résolu) Le calcul montre que pour le Pocket il y a 88179840 états.
Tout ce qui dit ici pour le Pocket, est valable aussi pour le Rubik's Cube. c'est-à-dire on oriente le Rubik's Cube comme on oriente le Pocket ... On trouve alors que le Rubik's Cube a 43 252 003 274 489 856 000 états
En 1993, Jerry Bryan écrivait un programe informatique pour calculer le diamètre du Pocket et a trouvé 14.
| distance | q |
|---|---|
| 0 | 1 |
| 1 | 12 |
| 2 | 114 |
| 3 | 924 |
| 4 | 6539 |
| 5 | 39528 |
| 6 | 199926 |
| 7 | 806136 |
| 8 | 2761740 |
| 9 | 8656152 |
| 10 | 22334112 |
| 11 | 32420448 |
| 12 | 18780864 |
| 13 | 2166720 |
| 14 | 6624 |
| total | 88179840 |
Les classes
Lors d'une compétition, l'état b est considéré comme l'état résolu. En fait l'état e et l'état b sont équivalents pour le jury.
Ainsi mathématiquement on classe les états dans une même classe (même boîte) suivant un certain critère Ici le critère est le groupe de déplacement, ou le groupe des isométries positives du Cube D(P). Ce groupe possède 24 éléments.
Deux états u et v sont équivalants s'il existe une rotation qui fait passer de u à v.
On montre alors qu'il y a 3674160 classes et chaque classe possède 24 éléments..
En effet toute permutation des 8 sommets est possible (8! positions), et 7 des sommets peuvent être orientés différemment (37 positions). L'orientation du Pocket dans l'espace n'a pas d'importance (pour un jury de compétitions) , ce qui donne le nombre de classes en divisant le nombre de positions par 24.
Le nombre de classes est donc :
- .
L'étude mathématique du Pocket revient en fait à étudier uniquement les « sommets » du Rubik's Cube
Il est possible de trouver toutes les classes informatiquement
Le tableau suivant indique le nombre de classes en f-métrique (A² compte 1) et le nombre de classes en q-métrique (A² compte 2)
Exemple : il y a 1847 classes à distance 4f , et 534 classes à distance 4q .
| distance | f | q |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 9 | 6 |
| 2 | 54 | 27 |
| 3 | 321 | 120 |
| 4 | 1 847 | 534 |
| 5 | 9 992 | 2 256 |
| 6 | 50 136 | 8 969 |
| 7 | 227 536 | 33 058 |
| 8 | 870 072 | 114 149 |
| 9 | 1 887 748 | 360 508 |
| 10 | 623 800 | 930 588 |
| 11 | 2 644 | 1 350 852 |
| 12 | 782 536 | |
| 13 | 90 280 | |
| 14 | 276 | |
| total | 3 674 160 | 3 674 160 |
Remarque : il se trouve que le diamètre du graphe des classes (14q) est le même que le diamètre du graphe d'états (14q).
e et b sont dans une même classe car on passe de e à b par une rotation.
Ces classes se nomment les iso+ classes
Il y a une grande différence entre un état et une classe
la classe cl(e) est un ensemble ayant 24 éléments, alors que e est un état une configuration des autocollants.
Comme les classes modulo 3 (il y a 3 classes)
1 est un nombre, la classe de 1, cl(1) est un ensemble infini d'éléments.
Résumé :
Le Rubik's Cube a: 43 252 003 274 489 856 000 états
Le Pocket a : 88179840 états.
On sait que l'ensemble des états forme un groupe et dans un groupe il y a un seul élément neutre e (état résolu) donc pour le Pocket mathématiquement on ne peut pas considérer b comme un état résolu .
Remarque importante :
Il est important de maîtriser le concept d'états. Un état est une configuration des autocollants provenant des rotations de base en respectant l'orientation du Cube.
Prenons un Rubik's Cube et un Pocket mélangés Posez le Rubik's Cube et le Pocket sur la table avec une face devant.
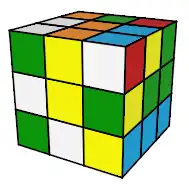 (a)
(a)
 (b)
(b)
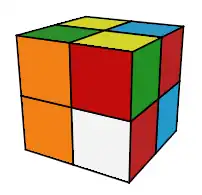 (c)
(c)
est ce que (a), (b), (c) sont des états ?? Pour le Rubik's Cube on a la réponse immédiatement
(a) = non, ce n'est pas un état
(b) = oui, c'est un état
(c) = on ne sait pas ! tout dépend du mélangeur, s'il y a mélangé le Pocket en gardant l'orientation du Cube càd sans tourner, sans bouger le Cube alors oui c'est un état, sinon, ce n'est pas un état.
C'est la différence entre le Rubik's Cube et le Pocket (c'est pareil avec le Revenge)
Pour le Pocket, le fait qu'on ne peut pas répondre immédiatement oui ou non une configuration est un état ou non , ceci rend la confusion entre les états et les classes du Pocket.
Records récents
| Temps | Compétiteur | Nationalité | Lieu | Date |
|---|---|---|---|---|
| 0 s 47 | Guanbo Wang | Northside Spring Saturday 2022 | 26 novembre 2022 | |
| 0 s 49 | Maciej Czapiewski | Grudziądz Open 2016 | 20 mars 2016 | |
| 0 s 58 | Rami Sbahi | Canadian Open 2015 | 7 juin 2015 | |
| Voir la suite ou | ||||
| Temps | Compétiteur | Nationalité | Lieu | Date |
|---|---|---|---|---|
| 1 s 01 | Zayn Khanani | Pioneer Valley Cubing B 2023 | 22 janvier 2023 | |
| 1 s 02 | Zayn Khanani | Cape Fear 2022 | 12 février 2022 | |
| 1 s 05 | Zayn Khanani | Finnish Championship 2021 | 30 octobre 2021 | |
| Voir la suite ou | ||||
La moyenne est calculée sur 5 tentatives en enlevant le meilleur et le moins bon temps.
Désignation des rotations
Dans tous les cubes la désignation est identique :
- Une lettre non suivie d'un prime signifie un quart de tour dans le sens des aiguilles d'une montre ;
- Une lettre suivie d'un prime signifie un quart de tour dans le sens inverse des aiguilles d'une montre ;
- La lettre est l'initiale de la rotation en anglais :
- (U)p = (H)aut, (D)own = (B)as, (F)ront = (A)vant, (B)ack = (P)ostérieur, (L)eft = (G)auche, (R)ight = (D)roite,
- le « 2 » signifie 180°.
Méthode de résolution
Une des méthodes les plus simples se décompose en 2 étapes :
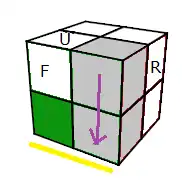
Finir le Bas
On commence par ranger les sommets-Bas
On va ranger les sommets-Bas dans l'ordre suivant: (DFR), (DRB), (DBL) et (DLF) :
1. Choisissez un sommet-Bas (jaune) , placez le en (URF), puis descendez le en (DFR)
a) Descendre: (URF)->(DFR) = RUR'U'
Si le sommet (BFR) n'est pas bien orienté, on l'oriente tout de suite par la formule
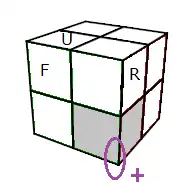
b) Pivoter dans le sens horaire: (DFR)+ = (RUR'U')²
2. Tourner le Cube entier suivant U, on cherche alors le sommet qui a les couleurs Bas et Avant
3. Revenez au point 1
Remarque: si le sommet cherché est en Bas on le remonte avec RUR'U' .
Finir le Haut
On commence par placer les sommets, puis on les oriente
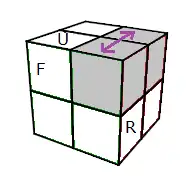
(URF)<->(UBR) = RUR'U' F'U'F
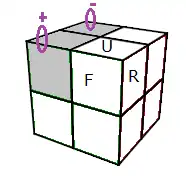
(UFL)+(ULB)- = (RUR'U')² .L' (URU'R')² L
Echanger deux sommets :
(URF)<->(UBR) = RUR'U' F'U'F
Pivoter deux sommets :
(UFL)+(ULB)- = (RUR'U')² .L' (URU'R')² L
Notes et références
- La moyenne est calculée sur cinq tentatives en enlevant le meilleur et le moins bon temps.


