Plan tangent

Le plan tangent en P à une surface Σ est une approximation de la surface au voisinage de P par un plan affine. Il a le même vecteur normal que cette surface. Si l'on dispose de ce vecteur normal, l'équation du plan tangent en découle puisqu'elle fait intervenir les composantes (x, y, z) des vecteurs qui sont, par définition, orthogonaux à ce vecteur.

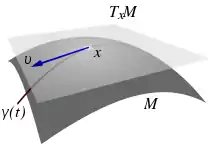
Le plan T_xM (gris clair) est tangent à la surface en M, selon le chemin orienté γ(t), passant par M où le vecteur ν est tangent au chemin.

En d'autres termes, si le vecteur ${\displaystyle {\vec {u}}}$ de composantes (a, b, c) est normal à la surface, tous les vecteurs ${\displaystyle {\vec {\mathrm {X} }}}$ de composantes (x, y, z) qui vérifient

${\displaystyle {\vec {\mathrm {X} }}\cdot {\vec {u}}=0}$

appartiennent au plan vectoriel tangent à la surface et réciproquement. Son équation est par conséquent

a⋅x + b⋅y + c⋅z = 0.

En géométrie différentielle, cette notion se généralise à celle d'espace tangent à une variété différentielle.