Orthogone de Lill

Considérons une équation cubique : ${\displaystyle ax^{3}+bx^{2}+cx+d=0}$

Pour l'illustration graphique, on choisit : ${\displaystyle x^{3}+6x^{2}+11x+6=0}$

Construction de l'orthogone.

La première étape est de construire l'orthogone de Lill. Le plan est doté d'un repère orthonormé ${\displaystyle 0,{\vec {u}},{\vec {v}}}$. À partir du point O, on construit des segments successifs, dont les longueurs correspondent aux coefficients du polynôme. Le segment OM est de longueur A et orienté selon ${\displaystyle {\vec {u}}}$. M se situerait donc à gauche de O si a était négatif. Le segment MN est de longueur b selon ${\displaystyle {\vec {v}}}$, et ainsi de suite : entre chaque segment on tourne de 90° dans le sens antihoraire.

Utilisation pour évaluer le polynône pour x= -0.5.

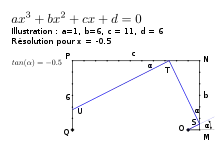
L'orthogone de Lill permet d'évaluer le polygone pour une valeur de x donnée. Ici, on l'illustre pour ${\displaystyle x=-0.5}$. On trace un premier segment OS. L'angle ${\displaystyle \alpha }$ entre OM et OS est tel que ${\displaystyle tan(\alpha )=-x=0.5}$ et S se situe sur la droite (MN). On vérifie aisément que : ${\displaystyle {\vec {MS}}=-xa{\vec {v}}}$

et donc : ${\displaystyle {\vec {SN}}\cdot {\vec {v}}=b+xa}$

Après le point S, la construction se poursuit avec un angle droit, jusqu'à croiser (NP) au point T. On retrouve le même angle ${\displaystyle \alpha }$.

On a donc : ${\displaystyle {\vec {NT}}\cdot {\vec {u}}=SN\times tan(\alpha )=-x(b+xa)=-ax^{2}-bx}$ Et ${\displaystyle {\vec {PT}}\cdot {\vec {u}}=c-(-ax^{2}-bx)=c+ax^{2}+bx}$

On réitère l'opération, avec un nouvel angle droit, et le tracé atteint la droite (PQ) au point U.

${\displaystyle {\vec {PT}}\cdot {\vec {v}}=PT\times tan(\alpha )=-x(c+ax^{2}+bx)=-ax^{3}-bx^{2}-cx}$

Et enfin, le vecteur QU, projecté selon ${\displaystyle {\vec {v}}}$, n'est autre que l'évaluation du polynôme pour x :

${\displaystyle {\vec {QU}}\cdot {\vec {v}}=d-(-ax^{3}-bx^{2}-cx)=ax^{3}+bx^{2}+cx+d}$

Notre polynôme admet trois racines.

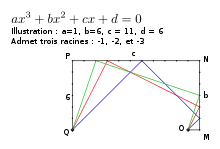
Résoudre l'équation, c'est donc trouver les angles alpha pour lesquels les points Q et U sont confondus. Dans le polynôme pris pour exemple, il y a trois racines, -1, -2, et -3. Les tracés correspondant sont illustrés en bleu, rouge et vert.

La mathématicienne italienne Margherita Piazzola Beloch a découvert et publié, en 1936, une méthode basée sur l'orthogone de Lill pour résoudre une équation cubique par origami. Elle a ainsi, prouvé pour la première fois que l'origami était un outil mathématique plus puissant que la construction à la règle et au compas, qui ne peut résoudre, au plus, qu'une équation quadratique[1].

• Cercle de Carlyle