Orthobicoupole octogonale
En géométrie, l'orthobicoupole octogonale est un des solides de Johnson (J28). Comme son nom l'indique, il peut être construit en joignant deux coupoles octogonales (J4) par leurs bases octogonales, en faisant coïncider leur faces identiques. Une rotation à 45 degrés d'une des coupoles avant la jonction donne une gyrobicoupole octogonale (J29).
| Orthobicoupole octogonale | |
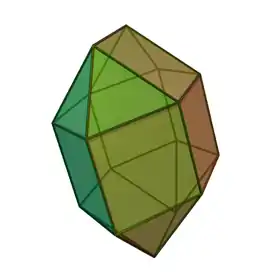
| |
| Type | Orthobicoupole J27 - J28 - J29 |
|---|---|
| Sommets | 16 |
| Arêtes | 32 |
| Faces | (nombre : 18) 8 t 10 c |
| Configuration faciale | 8 de 32.42 8 de 3.43 |
| Groupe symétrique | D4h |
| Dual | - |
| Propriétés | convexe |
L'orthobicoupole octogonale est le deuxième solide dans l'ensemble infini des orthobicoupoles.
L'orthobicoupole octogonale peut être allongée en insérant un prisme octogonal entre ses deux coupoles pour donner un rhombicuboctaèdre, ou effondrée par l'enlevement d'un prisme hexagonal irrégulier pour donner une dipyramide carrée allongée (J15), qui est simplement un octaèdre allongé.
Les 92 solides de Johnson ont été nommés et décrits par Norman Johnson en 1966.