Notation de Neveu

En théorie des graphes, un arbre planaire enraciné peut être décrit de manière non ambigüe par la liste de ses sommets, chacun désigné par une suite finie d'entiers, qui sont les positions, au sein de leur fratrie, des ancêtres du sommet : c'est la notation de Neveu[1].

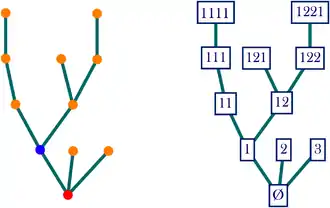
Notation de Neveu pour les sommets d'un arbre planaire.

On utilise ici l'arbre généalogique comme métaphore pour l'arbre planaire : le sommet 2|4|3 désigne le 3^e fils du 4^e fils du 2^e fils de l'ancêtre (l'ancêtre étant lui-même désigné par la suite vide, notée $\scriptstyle \emptyset \$ ). Par convention, l'ancêtre est le sommet initial de l'arête racine, et le sommet final de l'arête racine est le fils ainé de l'ancêtre : en tant que tel, il est noté 1. La longueur de la suite associée à un sommet est la hauteur (ou la profondeur) du sommet, i.e. la distance entre ce sommet et le début de la racine, qui représente l'ancêtre : en filant la métaphore, un sommet de hauteur n représente un individu appartenant à la n-ème génération de la population fondée par l'ancêtre.

Exemple

Les 5 arbres à 3 arêtes.

Exemple :

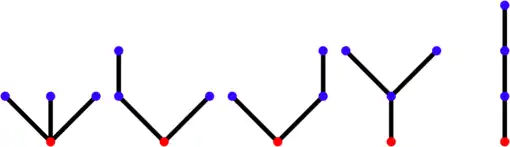
Les 5 arbres à 3 arêtes ci-dessus sont ainsi décrits par les 5 ensembles de mots ci-dessous :

\{\emptyset ,1,2,3\},\ \{\emptyset ,1,11,2\},\ \{\emptyset ,1,2,21\},\ \{\emptyset ,1,11,12\},\ \{\emptyset ,1,11,111\}.

Remarques

Le parcours des sommets dans l'ordre lexicographique est alors le parcours en profondeur préfixé (ou parcours préfixe) d'un arbre vu comme structure de données en informatique. Autre application : avec cette notation, un arbre planaire encode commodément une réalisation de processus de Galton-Watson avec extinction. Rien ne s'oppose à définir un arbre planaire infini à l'aide de la notation de Neveu, ce qui permet d'encoder les réalisations de processus de Galton-Watson où la population ne s'éteint pas.

Note et référence

J. Neveu, « Arbres et processus de Galton-Watson », Ann. de l'IHP, vol. 22, n^o 2,‎ 1986 (lire en ligne) (section 2).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.