Nombre parfait multiple

En mathématiques, un nombre parfait multiple (aussi appelé nombre multiparfait ou nombre plus-que-parfait) est une généralisation d'un nombre parfait.

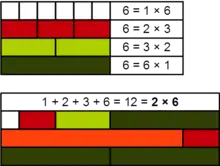
Démonstration, à l'aide de tiges Cuisenaire, de la 2-perfection du nombre 6

Pour un nombre naturel donné $k$ , un nombre $n$ est appelé $k$ -parfait si et seulement si la somme de tous les diviseurs positifs de $n$ , $\sigma (n)\,$ ) est égale à $kn$ ; ainsi, un nombre est parfait si et seulement si il est 2-parfait. Un nombre qui est $k$ -parfait pour un certain $k$ est appelé un nombre parfait multiple. Les nombres $k$ -parfaits sont connus pour chaque valeur de $k$ jusqu'à 11 (juillet 2004).

Il peut être démontré que :

Pour un nombre premier donné $p$ , si $n$ est p-parfait et p ne divise pas $n$ , alors $pn$ est ( $p$ + 1)-parfait. Ceci implique que si un entier $n$ est un nombre 3-parfait divisible par 2 mais pas par 4, alors $n$ /2 est un nombre parfait impair, pour lequel aucun n'est connu.
Si 3 $n$ est 4 $k$ -parfait et 3 ne divise pas $n$ , alors $n$ est 3 $k$ -parfait.

Plus petits nombres k-parfaits

La table suivante donne une vue d'ensemble des plus petits nombres $k$ -parfaits pour $k\leq 7\,$ (voir la suite A007539 de l'OEIS) :

k	Plus petit nombre k-parfait	Découvert par
1	1	anciens
2	6	anciens
3	120	anciens
4	30 240	René Descartes, environ 1638
5	14 182 439 040	René Descartes, environ 1638
6	154 345 556 085 770 649 600	Robert Daniel Carmichael, 1907
7	141 310 897 947 438 348 259 849 402 738 485 523 264 343 544 818 565 120 000	TE Mason, 1911

Liens externes

(en) Achim Flammenkamp, The Multiply Perfect Numbers Page
(en) Prime Pages' Glossary, Multiply perfect

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Multiply perfect number » (voir la liste des auteurs).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.