Nombre de Dottie
Le nombre de Dottie est une constante mathématique définie comme étant l'unique solution réelle de l'équation où est exprimé en radians. On l'obtient donc géométriquement comme abscisse et ordonnée du point d'intersection de la droite d'équation et de la courbe d'équation .
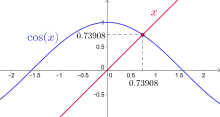
Une valeur approchée en est 0,739085133215[alpha 1], voir la suite A003957 de l'OEIS.
C'est l'unique point fixe de la fonction cosinus, point fixe qui est de plus attractif, et possède un bassin d'attraction égal à tout entier [1]. C'est la raison pour laquelle, lorsqu'on appuie plusieurs fois sur la touche "cos" d'une calculatrice (réglée en mode "radian"), quel que soit le nombre de départ, on obtient rapidement ce nombre, qui a donc été remarqué par de nombreux lycéens et étudiants.
Historique
Le nom "Dottie" est le surnom donné par Samuel Kaplan à une amie, professeur de français, qui avait remarqué la propriété étonnante sur sa calculatrice et en avait demandé la raison [2].

Propriétés
- Toutes les suites de premier terme réel et vérifiant convergent vers le nombre de Dottie.
- Le nombre de Dottie est transcendant d'après le théorème d'Hermite-Lindemann[3] - [alpha 2].
Applications
Le nombre de Dottie apparait dans peu de problèmes mathématiques ; il est principalement utilisé comme exemple de point fixe attractif par les professeurs de mathématiques. On trouvera des applications dans [4].
Valeurs trigonométriques liées à ce nombre
Appelons D le nombre de Dottie, on a :
Le fait que prouve l’attractivité de D comme point fixe.
Autres nombres similaires
- Si la calculatrice est réglée en mode "degré", le fait d'appuyer sur la touche "cos" conduit à l'unique solution de , de valeur approchée
0,99984774, voir la suite A330119 de l'OEIS. - Des appuis successifs sur les touches "racine carrée" ou "sin" conduisent respectivement vers 1 ou 0.
- Des appuis alternés sur les touches "sin" et "cos" conduisent au cycle attractif où est l'unique solution de , voir la suite A131691 de l'OEIS, et est l'unique solution de , voir la suite A277077 de l'OEIS
- L'unique solution entre 0 et de a pour valeur approchée 0,86033359, voir la suite A069855 de l'OEIS, mais ce point fixe n'est pas attractif. Il l'est par contre pour la fonction .
- L'unique solution entre et de a pour valeur approchée 4,493409, voir la suite A115365 de l'OEIS ; c'est aussi l'unique point fixe de , point fixe qui est attractif. C'est également l'abscisse du premier minimum pour de la fonction sinus cardinal : .
- L'unique solution positive de , a pour valeur approchée 1,19967864, voir la suite A085984 de l'OEIS, et ce point fixe est attractif. Notant cette constante, le nombre est la constante de Laplace.
- L'équation complexe possède des solutions complexes non réelles, de la forme où est solution de , voir la suite A335565 de l'OEIS et la suite A335566 de l'OEIS.
Bibliographie
- James Stewart Single Variable Calculus : Concepts and Contexts Brook/Cole 2010, (ISBN 978-0-495-55972-6), page 314
- Miller T.H. On the Numerical Values of the Roots of the Equation cos x = x Proc. Edimburg Math. Soc. 9, 1890, pages 80 à 83
- Bertrand J. Exercice III Traité d'Algèbre Vol 1-3, 4e édition Paris Librairie de L. Hachette et Cie, 1865, page 285
Notes et références
Notes
- Le site en russe de pikabu donne plus précisément comme valeur 0,739085 133215 160641 66... voir le lien http://pikabu.ru/story/kosinus_07390851332_1230436.
Une calculette d'ordinateur à 32 décimales donne le nombre 0,739085 133215 160641 655312 087673 87... - On note le nombre de Dottie. Supposons qu'il n'est pas transcendant. Il est donc algébrique et donc son produit par i aussi. De plus par définition, . Mais alors d'après le théorème d'Hermite-Lindemann, on a qui est transcendant. Or comme , est transcendant aussi, et n'est donc pas algébrique : on aboutit à une contradiction si l'on suppose algébrique. est donc transcendant.
Références
- François Rouvière, Petit guide de calcul différentiel, Cassini, , p. 160
- Samuel R Kaplan, « The Dottie Number », Mathematics Magazine, vol. 80, , p. 73 (lire en ligne, consulté le )
- (en) Eric W. Weisstein, « Dottie Number », sur MathWorld
- (en) Valerii Salov, « Inevitable Dottie Number. Iterals of cosine and sine », Arxiv, (lire en ligne)
Voir aussi
- Jérôme Cottanceau, « Les nombres magiques », sur Chou romanesco, vache qui rit et intégrales curvilignes,
- (en) [vidéo] What is cos( cos( cos( cos( cos( cos( cos( cos( cos( cos( cos( cos(…?? // Banach Fixed Point Theorem sur YouTube (consulté le )





































