Multiplieur

En électronique analogique, un multiplieur est un circuit dont le signal de sortie est le produit de la valeur instantanée de ses signaux d'entrée[1].

Un multiplieur peut être constitué d'un circuit amplificateur différentiel, dans lequel le courant de la branche commune détermine le gain différentiel ; il peut aussi exploiter l'effet Hall[2].

En radio, le multiplieur, essentiel à la modulation et à la démodulation hétérodyne, est construit autour d'un composant non linéaire (le plus souvent une diode.

Un multiplicateur de fréquence est un circuit non linéaire, auquel on applique un signal en bande étroite. Le signal résultant comporte de nombreuses harmoniques de la fréquence d'entrée. Un filtre sélectionne celle de ces fréquences multiples de celle du signal est présente en sortie[3].

Les algorithmes utilisés par les multiplieurs actuels sont des variantes améliorées de l’algorithme de multiplication à colonne appris dans les petites classes. La seule différence tient dans la table de multiplication utilisée. En binaire, cette table de multiplication se résume à celle-ci :

• ${\displaystyle 0\times 0=0}$
• ${\displaystyle 0\times 1=0}$
• ${\displaystyle 1\times 0=0}$
• ${\displaystyle 1\times 1=1}$

Pour le reste, l'algorithme est identique à celui appris en primaire. Celui-ci consiste à calculer des produits partiels, chacun étant égal au produit d'un des chiffres du multiplieur par le multiplicande. Ces produits partiels sont ensuite additionnés tous ensemble pour donner le résultat.

Multiplieur simple

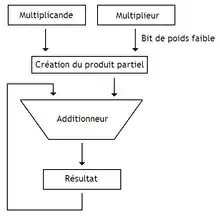
Les multiplieurs les plus simples implémentent l'algorithme vu au-dessus de la façon la plus triviale qui soit, en calculant les produits partiels et en les additionnant un par un. Ces multiplieurs sont donc composés d'un additionneur, et d'un accumulateur pour mémoriser les résultats temporaires. Ceux-ci incorporent des registres pour stocker le multiplicande et le multiplieur durant toute la durée de l'opération. L'ensemble est secondé d'un compteur, chargé de gérer le nombre de répétitions qu'il reste à effectuer avant la fin de la multiplication, et d'un peu de la logique combinatoire pour gérer le début de l’opération et sa terminaison.

Au tout début de l'opération, le multiplieur et le multiplicande sont stockés dans des registres, et l'accumulateur stockant le résultat est initialisé à zéro. Puis, à chaque cycle d'horloge, le multiplieur va calculer le produit partiel à partir du bit de poids faible du multiplieur, et du multiplicande. Ce calcul du produit partiel est un simple ET entre chaque bit du multiplicande, et le bit de poids faible du multiplieur. Ce produit partiel est alors additionné au contenu de l'accumulateur. À chaque cycle, le multiplieur est décalé d'un cran vers la droite, afin de passer au bit suivant (pour rappel, on effectue la multiplication du multiplicande par un bit du multiplieur à la fois). Le multiplicande est aussi décalé d'un cran vers la gauche.

Le multiplieur vu au-dessus peut subir quelques petites optimisations. Une première optimisation consiste à ne pas effectuer de produit entre multiplicande et bit de poids faible du multiplieur si ce dernier est nul. Dans ce cas, le produit partiel sera nul, et son addition avec le contenu de l'accumulateur inutile. On peut parfaitement se contenter de décaler le contenu du multiplicande, sans calculer le produit partiel et effectuer l'addition. Cela peut se faire assez simplement en utilisant la logique combinatoire reliée au circuit, à condition que celle-ci s'occupe de séquencer les décalages et de commander l'additionneur. De même, si le bit de poids faible du multiplieur n'est pas nul, il est inutile de faire le produit (via ET), le produit est identique au multiplicande.

Il suffit donc, à chaque cycle d'horloge, si le bit de poids faible du multiplieur n'est pas nul, d’additionner le multiplicande au contenu de l'accumulateur. À chaque cycle, le multiplieur est décalé d'un cran vers la droite, et le multiplicande est décalé d'un cran vers la gauche.

Multiplieur partagé

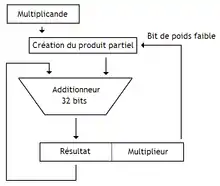
Une autre optimisation possible consiste à stocker le résultat en sortie de l'additionneur non pas dans les bits de poids faible de celui, mais dans ses bits de poids forts. Si on décale notre accumulateur d'un cran vers la droite à chaque addition de produit partiel, on peut obtenir le bon résultat. Avec cette technique, on peut utiliser un additionneur plus petit. Par exemple, sans cette optimisation, la multiplication de deux nombres de 32 bit demanderait un additionneur capable de traiter des nombres de 64 bits. Avec optimisation, un vulgaire additionneur 32 bits peut suffire.

Dans ce multiplieur optimisé, il est possible de fusionner le registre du multiplieur et l'accumulateur. L'astuce de ce circuit consiste à stocker le multiplieur dans les bits de poids faible du registre fusionné, et à placer le résultat en sortie de l'additionneur dans les bits de poids fort. À chaque cycle, le registre accumulateur est décalé vers la droite. Les bits utilisés par le multiplieur sont donc progressivement remplacés par le résultat des additions du produit partiel. Cette fusion permet d'utiliser un additionneur plus simple.

Multiplieur tableau

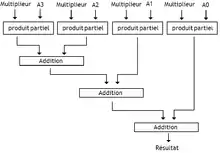
Au lieu d'additionner les produits partiels un par un, il est aussi possible de les effectuer en parallèle. Il suffit d'utiliser autant d'additionneurs et de circuits de calcul de produits partiels qu'il y a de produits partiels à calculer. On peut ainsi calculer tous les produits partiels en parallèle, et effectuer les additions avec un ensemble d'additionneurs reliés en série. Généralement, ce sont des additionneurs à propagation de retenue qui sont utilisés dans ce type de circuits. L'usage d'additionneurs plus évolués augmenterait beaucoup trop la quantité de portes logiques utilisée par le circuit final, pour un gain en performance assez faible.

Néanmoins, enchainer des additionneurs en série ainsi utilise beaucoup de circuits. Qui plus est, ces additionneurs possèdent un temps de propagation non négligeable. Les gains en termes de performance existent comparé aux multiplieurs vus au-dessus, mais ne méritent pas forcément une telle augmentation de la taille du circuit. Pour éviter de gaspiller la place, il est possible d'utiliser des additionneurs dits carry-save, conçus pour accélérer les additions multiples.

Réduction des produits partiels d'une multiplication à 8 bits par un arbre de Wallace

Pour gagner en performance, et rendre le circuit plus rapide, il est possible d'effectuer les additions de produits partiels non pas en série, mais via un arbre de réduction. Cet arbre tire parti du fait que trois bits de même poids dans les produits partiels peuvent être additionnés en deux bits, dont un de poids supérieur, et s'intéresse juste aux bits individuels des produits partiels sans chercher à additionner ceux-ci deux à deux. On économise ainsi la propagation de la retenue, qui est cause de latence et de complexité dans les additionneurs. Lorsqu'il n'est plus possible d'effectuer de réduction, on additionne les deux groupes de chiffres restants.

Pour deux nombres de taille n, comme le nombre de chiffres des produits partiels est n² au total et que la réduction prend un nombre d'étapes logarithmique, les arbres de réduction permettent d'effectuer la multiplication en un temps ${\displaystyle O(\log n)}$, comme c'est le cas pour l'addition. Cependant, les multiplieurs sont en pratique plus lents et imposants que les additionneurs.

Il existe divers types d'arbres permettant d'effectuer la réduction, les plus connus étant les arbres de Wallace ainsi que les arbres Dadda.