Modèle de Goodwin

Proposé par l'économiste américain Richard Goodwin en 1967, le modèle de Goodwin combine des aspects du modèle de croissance de Harrod et Domar avec la courbe de Phillips [1]. Ce modèle propose une description de cycles économiques qui sont endogènes à l'activité économique, c'est-à-dire que les causes des fluctuations sont déjà présentes au sein même de l'économie. A contrario, un choc exogène serait dû à une variable imprévue et extérieure (une innovation technologique qui vient soudainement bouleverser la donne, par exemple)[2].

Le modèle de Goodwin est surnommé « modèle de lutte des classes » car il se fonde sur l'antagonisme entre les détenteurs du capital (les capitalistes) et les détenteurs de la force de travail (les salariés). Le modèle met en scène deux grandes variables : le taux d'emploi et la part des salaires dans le revenu national. Lorsque le revenu des salariés dans le revenu national est faible, l'investissement (égal au profit) est soutenu, ce qui permet une croissance forte et une baisse du chômage. Or, la main d’œuvre étant finie, il arrive un moment où le stock de travailleurs disponible est épuisé. Les salaires augmentent donc, car la pénurie donne un pouvoir de négociation plus fort aux salariés. Comme la valeur ajoutée va de plus en plus aux salariés, la part dédié au capital s'érode, ce qui ralentit et réduit l'investissement ; cela réduit nécessairement la croissance, et fait donc augmenter le chômage. Le cycle est par conséquent relancé[2].

Les postulats du modèle sont les suivants : le marché des biens est toujours équilibrés ; les profits sont épargnés et réinvestis ; les salaires sont consommés ; le marché du travail est déséquilibré ; le taux de croissance du salaire réel dépend du chômage (en vertu de la courbe de Philips)[2].

Ce modèle explique les cycles de longue période, car, dans l'économie réelle, les salaires mettent du temps à s'adapter et s'ajuster au chômage[2].

La production est donnée par la fonction de production agrégée ${\displaystyle q=\min \left(a\ell ,{\frac {k}{\sigma }}\right)}$, où :

• q est la production agrégée ;
• ℓ est l'utilisation du travail ;
• k est le capital (homogène) ;
• a est la productivité du travail ;
• σ est le ratio capital-production, une constante.

Toutes ces variables sont fonction du temps, bien que les indices de temps aient été supprimés par commodité.

Contrairement au modèle Harrod-Domar, on suppose une utilisation complète du capital. Par conséquent, ${\displaystyle a\ell ={\frac {k}{\sigma }}=q}$ en tout temps. Le taux d'emploi est donné par ${\displaystyle v={\frac {\ell }{n}}}$, où n est la population active totale qui croît au taux β . De plus, la productivité du travail a, est supposée augmenter également au taux α. Notons que dans ce cas, le taux de croissance du taux d'emploi est donné par ${\displaystyle {\frac {dv/dt}{v}}=g_{v}=g_{\ell }-\beta }$.

Le taux de croissance du niveau absolu de l'emploi est à son tour donné par ${\displaystyle {\frac {d\ell /dt}{\ell }}=g_{\ell }=g_{q}-\alpha }$.

On suppose que les salaires changent selon une relation de courbe de Phillips linéarisée donnée par ${\displaystyle {\frac {dw/dt}{w}}=g_{w}=\rho v-\gamma }$.

En d'autres termes, si le marché du travail est « serré » (l'emploi est déjà élevé), il y a une pression à la hausse sur les salaires et vice versa dans un marché du travail «laxiste». C'est l'aspect du modèle qui peut être vaguement associé à la partie «lutte de classe» de son nom, cependant, ce type de courbe de Phillips peut être trouvé dans de nombreux modèles macroéconomiques.

La part des travailleurs dans la production est u, qui par définition est ${\displaystyle u={\frac {w\ell }{q}}={\frac {w}{a}}}$.

Par conséquent, le taux de croissance de la part des travailleurs est ${\displaystyle {\frac {du/dt}{u}}=g_{u}=g_{w}-\alpha }$.

La part du travail dans la production augmente avec les salaires mais diminue avec la croissance de la productivité car il faut moins de travailleurs pour produire la même quantité de production.

Enfin, nous avons l'équation d'accumulation du capital et le taux de croissance de la production qui en résulte (puisque k et q croissent au même taux en supposant une pleine utilisation du capital et des rendements d'échelle constants). On suppose que les travailleurs consomment leurs salaires et que les propriétaires du capital épargnent une partie de leurs profits (à noter que le modèle se généralise au cas où les capitalistes épargnent plus que les travailleurs) et que le capital se déprécie au delta des taux. Le taux de croissance de la production et du capital est alors donné par ${\displaystyle {\frac {dk/dt}{k}}=g_{k}=g_{q}=s(1-u)(q/k)-\delta }$.

Cela implique à son tour que ${\displaystyle {\frac {dv/dt}{v}}=g_{v}={\frac {s(1-u)}{\sigma }}-(\delta +\alpha +\beta )}$.

Les deux équations différentielles

${\displaystyle {\frac {dv/dt}{v}}=g_{v}={\frac {s(1-u)}{\sigma }}-(\delta +\alpha +\beta )}$

${\displaystyle {\frac {du/dt}{u}}=g_{u}=\rho v-\gamma -\alpha }$

sont les équations clés du modèle et sont en fait les équations Lotka-Volterra (qui sont utilisées en biologie pour modéliser l'interaction prédateur-proie).

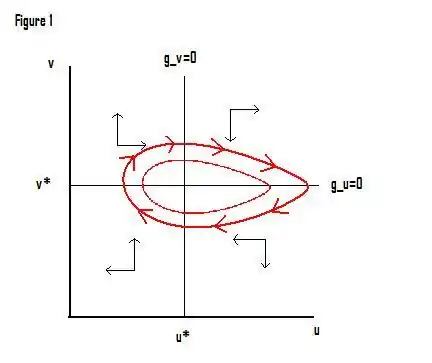
Bien que le modèle puisse être résolu explicitement, il est intéressant d'analyser la trajectoire de l'économie en termes de diagramme de phase. En définissant les deux équations ci-dessus égales à zéro, nous obtenons les valeurs de u et v pour lesquelles la croissance de v et la croissance u, respectivement, sont nulles.

${\displaystyle u*=1-{\frac {(\delta +\alpha +\beta )\sigma }{s}}}$

${\displaystyle v*={\frac {\gamma +\alpha }{\rho }}}$

Ces deux lignes (ainsi que les restrictions de paramètres qui garantissent que ni u ni v ne peuvent dépasser 1) divisent l'orthant positif en quatre régions. La figure ci-dessous indique avec des flèches le mouvement de l'économie dans chaque région. Par exemple, dans la région nord-ouest (emploi élevé, faible part du travail dans la production), l'économie se déplace vers le nord-est (l'emploi augmente, la part des travailleurs augmente). Une fois qu'il aura franchi la ligne u*, il commencera à se déplacer vers le sud-ouest.

La figure ci-dessous illustre l'évolution de la production potentielle (production au plein emploi), de la production réelle et des salaires au fil du temps.

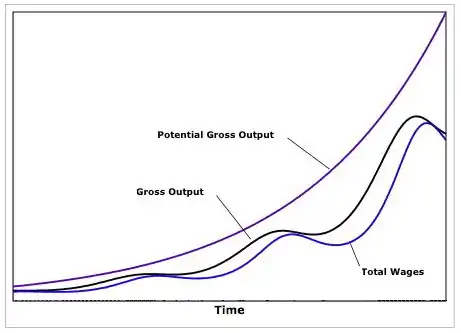
Comme on peut le voir, le modèle de Goodwin peut générer des fluctuations endogènes de l'activité économique sans s'appuyer sur des hypothèses étrangères de chocs extérieurs, que ce soit du côté de la demande ou de l'offre.

Le modèle a été appliqué et étendu par de nombreux économistes depuis sa première présentation en 1967.

• 
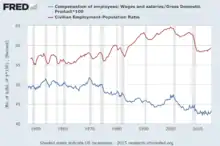  Part des salaires (ligne bleue) et taux d'emploi (ligne rouge) aux États-Unis. Selon le modèle de Goodwin, la part des salaires devrait être inférieure au taux d'emploi. Cela semble être le cas ne serait-ce que par un petit décalage dans le temps

Le modèle de Goodwin a connu une fertilité certaine dans les années qui ont suivi sa publication. Il a été utilisé pour expliquer la dynamique de la désinflation compétitive. Lorsqu'il y a du chômage, les salaires croissent moins vite, stagnent ou chutent, ce qui augmente la compétitivité des entreprises et leur profitabilité ; ces gains assurent une hausse de l'investissement, à un redémarrage de la croissance, et donc à une réduction du chômage[2].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Goodwin model (economics) » (voir la liste des auteurs).