Masse modale

La vibration d'une pièce peut se décomposer en mode de déformation élémentaires ; on parle de décomposition en harmoniques. Les images ci-dessous montrent quelques modes de déformation d'une peau de tambour.

• 
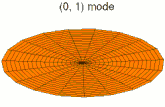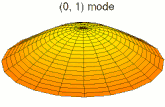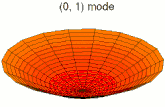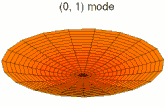  Mode k = 0, p = 1
• 
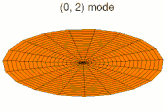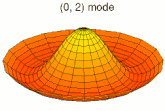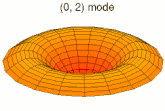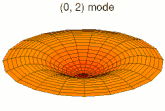  Mode k = 0, p = 2
• 
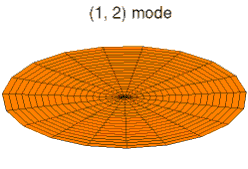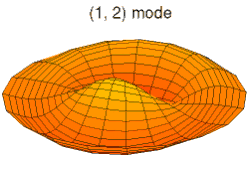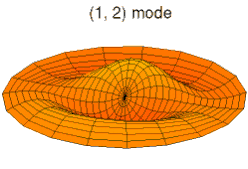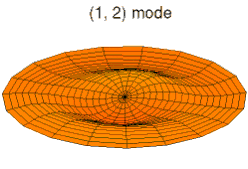  Mode k = 1, p = 2

Système masse-ressort oscillant.

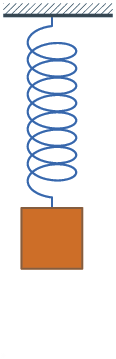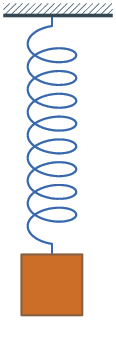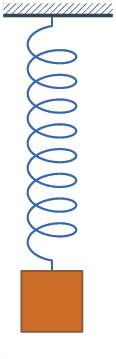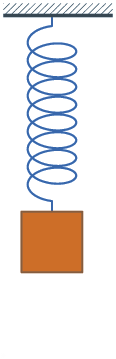
D'un point de vue de la dynamique, chaque mode i peut se représenter par un système masse-ressort (avec ou sans amortissement) : le système masse-ressort équivalent suit la même loi de comportement que la pièce que l'on étudie, et en particulier, il a la même fréquence propre.

La raideur du ressort équivalent k est la raideur de la pièce étudiée pour le même mode de déformation ; on peut l'obtenir avec un essai mécanique simple (traction, flexion) ou par calcul par éléments finis. La masse équivalente est alors la masse donnant au système masse-ressort la même fréquence que la fréquence du mode i considéré de la pièce

${\displaystyle f_{i}={\frac {1}{2\pi }}{\sqrt {\frac {k}{m_{i}}}}\Longrightarrow m_{i}={\frac {k}{4\pi ^{2}f_{i}^{2}}}}$.

Cette masse équivalente m_i est appelée masse modale.

On peut la voir comme la quantité de matière de la pièce qui contribue à la vibration, puisque certaines parties de la pièce se déplacent beaucoup et d'autres peu.