Marche de Jarvis
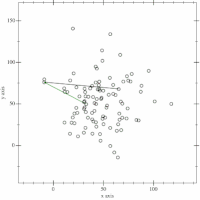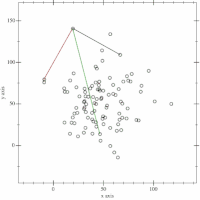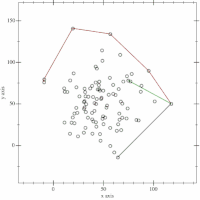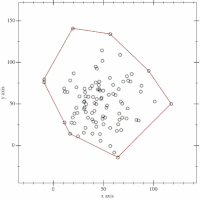
En géométrie algorithmique, la marche de Jarvis[1] est un algorithme pour calculer l'enveloppe convexe d'un ensemble fini de points. L'idée de l'algorithme est d' « envelopper » l'ensemble de points dans un « papier cadeau » : on accroche ce papier à l'un des points, on le tend, puis on tourne autour du nuage de point.
Principe

Soit le point initial, par exemple le point d'abscisse minima, où on accroche le papier.
Le premier point rencontré par le papier sera , puis ... jusqu'à retrouver .
Plus formellement, il s'agit pour chaque nouveau sommet de l'enveloppe convexe trouvé, de chercher le suivant en calculant le point d'angle polaire minimal par rapport à .
En pratique, on divise le parcours en deux : à partir du point d'abscisse minimale, puis à partir du point d'abscisse maximale.
L'algorithme
fonction marcheJarvis(E)
p := un point d'abscisse minimale dans E
L := liste vide
répéter
insérer p dans L
p := point p' de E tel que [pp') est le plus incliné vers la gauche (1)
jusqu’à p = p0
retourner L
La ligne (1) s'effectue de la manière suivante :
pointAGauche = premier point de E
pour tout pointCandidat de E
Si pointAGauche = p ou pointCandidat est à gauche du segment entre p et pointAGauche alors
pointAGauche=pointCandidat
p := pointAGauche
Le cas pointAGauche=p est une situation assez rare, qui peut intervenir lorsqu'on étudie le second point candidat de E, et qu'aucun meilleur pointAGauche n'a encore été trouvé dans la boucle. Le corps de la boucle répéter - jusqu'à est exécuté autant de fois qu'il y a de points dans l'enveloppe convexe. La ligne (1) est en . D'où une complexité en , où représente le nombre de sommets de l'enveloppe convexe.
Complexité
La boucle interne vérifie tous les point dans l'ensemble E, et la boucle externe se répète pour chaque point de l'enveloppe. Donc le nombre total de tour de boucle est en . Le temps d'exécution dépend de la taille de la sortie, on dit alors qu'il s'agit d'un algorithme sensible à la sortie.
Cependant, comme le temps d'exécution dépend linéairement du nombre d'arêtes de l'enveloppe, la marche de Jarvis peut être plus rapide que des algorithmes en (comme Parcours de Graham) lorsque le nombre h d'arêtes de l'enveloppe est plus petit que . L'algorithme de Chan, un autre algorithme d'enveloppe convexe, combine la dépendance logarithmique de l'algorithme de Graham avec la sensibilité à la sortie de la marche de Jarvis, lui permettant d'atteindre une complexité en temps en .
Notes et références
- R. A. Jarvis, « On the identification of the convex hull of a finite set of points in the plane », Information Processing Letters, vol. 2, , p. 18–21 (DOI 10.1016/0020-0190(73)90020-3, lire en ligne, consulté le )









