Méthode de discrétisation du gradient
En analyse numérique, la méthode de discrétisation du gradient (MDG) est un cadre incluant des schémas numériques classiques et récents pour approcher une variété de problèmes de type diffusion, qu'ils soient linéaires ou non, transitoires ou stationnaires. Ces schémas peuvent être conformes ou non, et peuvent être basés sur une discrétisation en espace polygonale ou polyédrique (mais on peut aussi considérer des méthodes d'approximation sans maillage).
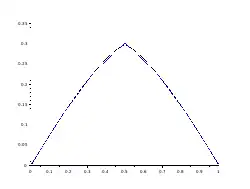
La preuve de la convergence d'un schéma élaboré au moyen de la MDG, pour approcher un problème elliptique ou parabolique linéaire ou non, repose sur un petit nombre de propriétés. Dans le cas d'un problème linéaire (stationnaire ou transitoire), il est possible d'établir une estimation d'erreur à l'aide de trois indicateurs propres à la MDG[1]. Dans le cas de certains problèmes non-linéaires, les preuves font appel à des techniques de compacité, sans pour autant nécessiter d'hypothèse forte sur la régularité de la solution du problème continu[2]. Les modèles non-linéaires pour lesquels une telle preuve de convergence de la MDG a pu être établie sont par exemple le problème de Stefan (qui modélise un matériau changeant d'état thermodynamique), les écoulements diphasiques en milieu poreux, l'équation de Richards (qui modélise l'écoulement de l'eau dans les sous-sols en présence d'air), le modèle de Leray—Lions[3].
Pour ces problèmes, il suffit qu'un schéma numérique entre dans le cadre de la MDG pour que la preuve de sa convergence soit établie. Cela s'applique ainsi aux méthodes de type Galerkine, aux éléments finis mixtes, aux éléments finis non conformes, et, dans le cas de schémas numériques plus récents, aux méthodes de Galerkine discontinues, aux méthodes hybrides mixtes mimétiques éventuellement nodales, à certaines méthodes de volumes finis en dualité discrète, et à certains schémas d'approximation multi-points des flux.
Un exemple : un problème de diffusion linéaire
On considère l'équation de Poisson dans un domaine ouvert borné , avec des conditions aux limites de Dirichlet homogènes
dans laquelle . La solution de ce modèle au sens faible usuel[4] est caractérisée par :
D'une manière générale, la MDG pour un tel modèle revient à définir un espace vectoriel de dimension finie, ainsi que deux opérateurs linéaires de reconstruction (l'un pour la fonction, l'autre pour son gradient), et à substituer ces objets discrets aux objets continus correspondants dans (2). Ainsi, la MDG passe par la définition d'une Discrétisation de Gradient (DG), définie par un triplet , dans lequel :
- l'ensemble des inconnues discrètes est un espace vectoriel de dimension finie (a priori sur le corps des réels),
- l'opérateur de reconstruction de la fonction est une application linéaire donnant, pour tout élément de , une fonction sur ,
- l'opérateur de reconstruction du gradient est une application linéaire donnant, pour tout élément de , une fonction vectorielle sur destinée à approcher le gradient de la fonction. Une propriété requise sur la reconstruction du gradient est que définisse une norme sur .
Le "schéma gradient" résultant pour l'approximation de (2) est donné par :
La MDG aboutit dans ce cas à une méthode d'approximation non conforme du problème (2), incluant les méthodes d'éléments finis non conformes. Il est important de remarquer que le cadre des MDG est cependant plus large, car il contient des méthodes qui ne peuvent pas être vues comme des éléments finis non conformes, par exemple pour lesquelles la fonction ne peut pas être obtenue à partir de la fonction .
L'estimation d'erreur ci-dessous est inspirée du second lemme de Strang[5] :
et
en définissant :
qui est une mesure de la coercivité (constante de Poincaré discrète),
qui est une mesure de l'erreur d'interpolation,
qui est une mesure de l'erreur de conformité.
Il est alors possible d'établir les bornes inférieure et supérieure ci-dessous pour l'erreur du schéma
Les propriétés nécessaires et suffisantes pour que la MDG converge sont ainsi, pour une famille de DGs, la coercivité, la DG-consistance et la conformité à la limite (dans les sens précisés dans le paragraphe suivant). De façon plus générale, ces trois propriétés sont suffisantes pour établir la convergence de la MDG pour des problèmes linéaires et pour certains problèmes non linéaires tels que celui du -Laplacien. Pour des problèmes non linéaires de diffusion (avec ou non dégénérescence de l'opérateur de diffusion), des propriétés supplémentaires peuvent être nécessaires (voir paragraphe suivant).
Propriétés permettant la convergence d'une MDG
Soit une famille de DGs, définies comme dans le paragraphe précédent (ces méthodes sont la plupart du temps associées à une suite de maillages dont le pas tend vers 0).
- Coercivité
La suite (définie par (6)) est bornée.
- DG-consistance
Pour tout , (défini par (7)).
- Conformité à la limite
Pour tout , (défini par (8)). Cette propriété implique la propriété de coercivité.
- Compacité (nécessaire pour certains problèmes non linéaires)
Pour toute suite telle que pour tout et reste borné, la suite est relativement compacte dans l'espace (cette propriété implique également la propriété de coercivité).
- Reconstruction constante par morceaux (nécessaire pour certains problèmes non linéaires)
L'opérateur est une reconstruction constante par morceaux s'il existe une base de et une famille de sous-ensembles disjoints de tels que pour tout , où est la fonction caractéristique de .
Quelques problèmes non linéaires pour lesquels la MDG converge
Il existe plusieurs problèmes pour lesquels une preuve de la convergence de la MDG a été établie lorsque certaines ou la totalité des propriétés ci-dessus sont satisfaites. On précisera pour chaque cas les propriétés nécessaires.
Problèmes de diffusion stationnaire non linéaire
Pour ce problème, les propriétés nécessaires à la preuve de la convergence de la MDG sont la coercivité, la DG-consistance, la conformité à la limite et la compacité.
Problème du p-laplacien avec p > 1
Pour ce problème, il convient de remplacer par , par et par avec , dans l'écriture des propriétés que la MDG doit vérifier. La convergence de la MDG est alors prouvée en supposant que les propriétés de coercivité, de DG-consistance et de conformité à la limite sont vérifiées.
Équation de la chaleur linéaire et non linéaire
Dans ce cas, la convergence de la MDG repose sur l'hypothèse que les propriétés de coercivité, de DG-consistance (étendue aux problèmes d'évolution), de conformité à la limite et de compacité (dans le cas non linéaire) sont satisfaites.
Problèmes paraboliques dégénérés
En supposant que et sont deux fonctions lipschitziennes croissantes au sens large, ce problème s'écrit :
Dans ce cas, la propriété de reconstruction constante par morceaux est nécessaire en plus des propriétés nécessaires aux problèmes de diffusion non linéaire.
Des méthodes numériques qui sont des MDG
Toutes les méthodes listées ci-dessous satisfont les premières quatre propriétés d'une MDG (coercivité, DG-consistance, conformité à la limite et compacité), et dans certains cas la cinquième (reconstruction constante par morceaux).
Méthode de Galerkine et d'éléments finis conformes
Soit l'espace vectoriel engendré par la base finie . La méthode de Galerkine dans est identique à la MDG définie par
Dans ce cas, la grandeur est la constante de l'inégalité de Poincaré continue, et, pour tout , (défini par (8)). Alors (4) et (5) sont déduits du lemme de Céa.
La technique dite de condensation de la masse pour une méthode d'éléments finis conforme est simplement décrite dans le cadre de la MDG, car elle consiste alors à remplacer par , où est une maille duale associée au degré de liberté . On obtient ainsi une DG satisfaisant la propriété de reconstruction constante par morceaux.
Éléments finis non conformes
Sur un maillage conforme de triangles ou de tétraèdres, la méthode d'éléments finis non conformes est définie par l'espace des fonctions affines par élément et continues au centre de gravité des faces du maillage (ces éléments finis sont en particulier utilisés par [Crouzeix et al][6] pour l'approximation des problèmes de Stokes et de Navier-Stokes). La méthode est alors une DG, en définissant la reconstruction du gradient au sein de chaque maille par le gradient de la fonction affine dans cette maille.
Éléments finis mixtes
La méthode des éléments finis mixtes repose sur la définition de deux espaces discrets, destinés l'un à l'approximation de et l'autre à l'approximation de [7]. Il suffit alors d'utiliser les relations discrètes entre ces approximations pour définir une DG. Les éléments finis de Raviart–Thomas de plus bas degré conduisent alors à la propriété de reconstruction constante par morceaux.
Méthode de Galerkine discontinue
La méthode de Galerkine discontinue pour des problèmes de diffusion consiste à approcher la solution par une fonction polynomiale par morceau, sans contraintes sur la discontinuité de la fonction qui en résulte sur les faces du maillage[8]. Cette méthode peut alors être vue comme une DG en définissant une régularisation du gradient de la fonction au sens des distributions.
Différences finies mimétiques et nodales
Ces familles de méthodes ont été introduites par [Brezzi et al][9] et étudiées plus complètement dans [Lipnikov et al][10]. Elles s'appliquent à des maillages polygonaux ou polyédriques généraux. L'identification de ces méthodes comme DGs est faite dans [Droniou et al][2].
Bibliographie
- (en) R. Eymard, C. Guichard et R. Herbin, « Small-stencil 3d schemes for diffusive flows in porous media », M2AN, vol. 46, , p. 265–290
- (en) J. Droniou, R. Eymard, T. Gallouët et R. Herbin, « Gradient schemes: a generic framework for the discretisation of linear, nonlinear and nonlocal elliptic and parabolic equations », Math. Models Methods Appl. Sci. (M3AS), vol. 23, no 13, , p. 2395–2432
- J. Leray et J. Lions, « Quelques résultats de Višik sur les problèmes elliptiques non linéaires par les méthodes de Minty-Browder », Bull. Soc. Math. France, vol. 93, , p. 97–107.
- (en) Haïm Brezis, Functional analysis, Sobolev spaces and partial differential equations, New York, Springer, coll. « Universitext »,
- (en) G. Strang, « Variational crimes in the finite element method : In The mathematical foundations of the finite element method with applications to partial differential equations », Proc. Sympos., Université de Maryland, Baltimore, Md., Academic Press, , p. 689–710
- (en) M. Crouzeix et P.-A. Raviart, « Conforming and nonconforming finite element methods for solving the stationary Stokes equations », I. Rev. Française Automat. Informat. Recherche Opérationnelle Sér. Rouge, vol. 7, no R-3, , p. 33–75
- (en) P.-A. Raviart et J. M. Thomas, « A mixed finite element method for 2nd order elliptic problems : In Mathematical aspects of finite element methods (Proc. Conf., Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975) », Lecture Notes in Math., Berlin, Springer, vol. 606, , p. 292–315
- (en) D. A. Di Pietro et A. Ern, « Mathematical aspects of discontinuous Galerkin methods », Mathématiques & Applications, Heidelberg, Springer, vol. 69,
- (en) F. Brezzi, K. Lipnikov et M. Shashkov, « Convergence of the mimetic finite difference method for diffusion problems on polyhedral meshes », SIAM J. Numer. Anal., vol. 43, no 5, , p. 1872–1896
- (en) K. Lipnikov, G. Manzini et M. Shashkov, « Mimetic finite difference method », J. Comput. Phys., vol. 257, no Part B, , p. 1163–1227
Liens externes
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gradient discretisation method » (voir la liste des auteurs).
- The Gradient Discretisation Method par Jérôme Droniou, Robert Eymard, Thierry Gallouët, Cindy Guichard et Raphaèle Herbin

![{\displaystyle \quad \quad \quad -|x-0.5|^{4/3}]}](https://img.franco.wiki/i/c882ae6f54227f78c5da52917a405f983ce40a2a.svg)


















![{\displaystyle \quad (9){\frac {1}{2}}[S_{D}({\overline {u}})+W_{D}(\nabla {\overline {u}})]\leq \left\Vert {\overline {u}}-\Pi _{D}u_{D}\right\Vert _{L^{2}(\Omega )}+\left\Vert \nabla {\overline {u}}-\nabla _{D}u_{D}\right\Vert _{L^{2}(\Omega )^{d}}\leq (C_{D}+2)[S_{D}({\overline {u}})+W_{D}(\nabla {\overline {u}})].}](https://img.franco.wiki/i/4f9f50f4bc5913dfad4429d61d0c338ecb7e083a.svg)












































