Loi normale asymétrique
En théorie des probabilités et en statistiques , la distribution normale asymétrique est une loi de probabilité continue qui généralise la distribution normale en introduisant une asymétrie non nulle.
Distribution normale asymétrique
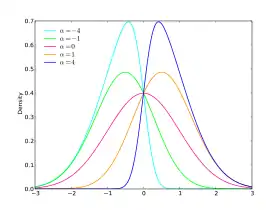
Densité de probabilité
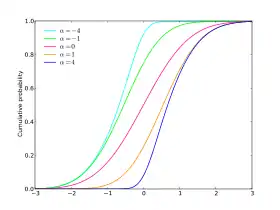
Fonction de répartition
Paramètres
ξ
{\displaystyle \xi \,}
position (réel )
ω
{\displaystyle \omega \,}
échelle (réel positif)
α
{\displaystyle \alpha \,}
forme (asymétrie ) (réel )
Support
x
∈
(
−
∞
;
+
∞
)
{\displaystyle x\in (-\infty ;+\infty )\!}
Densité de probabilité
1
ω
π
e
−
(
x
−
ξ
)
2
2
ω
2
∫
−
∞
α
(
x
−
ξ
ω
)
e
−
t
2
2
d
t
{\displaystyle {\frac {1}{\omega \pi }}e^{-{\frac {(x-\xi )^{2}}{2\omega ^{2}}}}\int _{-\infty }^{\alpha \left({\frac {x-\xi }{\omega }}\right)}e^{-{\frac {t^{2}}{2}}}\ dt}
Fonction de répartition
Φ
(
x
−
ξ
ω
)
−
2
T
(
x
−
ξ
ω
,
α
)
{\displaystyle \Phi \left({\frac {x-\xi }{\omega }}\right)-2T\left({\frac {x-\xi }{\omega }},\alpha \right)}
T
(
h
,
a
)
{\displaystyle T(h,a)}
fonction T d'Owen
Espérance
ξ
+
ω
δ
2
π
{\displaystyle \xi +\omega \delta {\sqrt {\frac {2}{\pi }}}}
δ
=
α
1
+
α
2
{\displaystyle \delta ={\frac {\alpha }{\sqrt {1+\alpha ^{2}}}}}
Variance
ω
2
(
1
−
2
δ
2
π
)
{\displaystyle \omega ^{2}\left(1-{\frac {2\delta ^{2}}{\pi }}\right)}
Asymétrie
4
−
π
2
(
δ
2
/
π
)
3
(
1
−
2
δ
2
/
π
)
3
/
2
{\displaystyle {\frac {4-\pi }{2}}{\frac {\left(\delta {\sqrt {2/\pi }}\right)^{3}}{\left(1-2\delta ^{2}/\pi \right)^{3/2}}}}
Kurtosis normalisé
2
(
π
−
3
)
(
δ
2
/
π
)
4
(
1
−
2
δ
2
/
π
)
2
{\displaystyle 2(\pi -3){\frac {\left(\delta {\sqrt {2/\pi }}\right)^{4}}{\left(1-2\delta ^{2}/\pi \right)^{2}}}}
Fonction génératrice des moments
2
exp
(
μ
t
+
σ
2
t
2
2
)
Φ
(
σ
δ
t
)
{\displaystyle 2\exp \left(\mu \,t+\sigma ^{2}{\frac {t^{2}}{2}}\right)\Phi (\sigma \delta t)}
Fonction caractéristique
exp
(
μ
i
t
−
σ
2
t
2
2
)
(
1
+
i
erf
(
σ
δ
t
2
)
)
{\displaystyle \exp \left(\mu \,i\,t-{\frac {\sigma ^{2}t^{2}}{2}}\right)\left(1+i\,\operatorname {erf} \left({\frac {\sigma \delta t}{\sqrt {2}}}\right)\right)}
Définition Soit
ϕ
(
x
)
{\displaystyle \phi (x)}
densité de probabilité de la loi normale centrée réduite
ϕ
(
x
)
=
1
2
π
e
−
x
2
2
{\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}}
avec sa fonction de répartition donnée par
Φ
(
x
)
=
∫
−
∞
x
ϕ
(
t
)
d
t
=
1
2
[
1
+
erf
(
x
2
)
]
{\displaystyle \Phi (x)=\int _{-\infty }^{x}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}
avec erf la fonction d'erreur .
Alors la densité de probabilité de la distribution normale asymétrique de paramètre α est donnée par
f
(
x
)
=
2
ϕ
(
x
)
Φ
(
α
x
)
.
{\displaystyle f(x)=2\phi (x)\Phi (\alpha x).\,}
Pour ajouter un paramètre de position et un paramètre d'échelle à cela, on utilise la transformation usuelle
x
↦
x
−
ξ
ω
{\displaystyle x\mapsto {\frac {x-\xi }{\omega }}}
α
=
0
{\displaystyle \alpha =0}
α
{\displaystyle \alpha }
α
>
0
{\displaystyle \alpha >0}
α
<
0
{\displaystyle \alpha <0}
f
(
x
)
=
(
2
ω
)
ϕ
(
x
−
ξ
ω
)
Φ
(
α
(
x
−
ξ
ω
)
)
.
{\displaystyle f(x)=\left({\frac {2}{\omega }}\right)\phi \left({\frac {x-\xi }{\omega }}\right)\Phi \left(\alpha \left({\frac {x-\xi }{\omega }}\right)\right).\,}
Estimation L'estimateur du maximum de vraisemblance pour
ξ
{\displaystyle \xi }
ω
{\displaystyle \omega }
α
{\displaystyle \alpha }
α
=
0
{\displaystyle \alpha =0}
méthode des moments peut être appliquée pour estimer
α
{\displaystyle \alpha }
|
δ
|
=
π
2
|
γ
^
3
|
2
3
|
γ
^
3
|
2
3
+
(
(
4
−
π
)
/
2
)
2
3
{\displaystyle |\delta |={\sqrt {\frac {\pi }{2}}}{\frac {|{\hat {\gamma }}_{3}|^{\frac {2}{3}}}{\sqrt {|{\hat {\gamma }}_{3}|^{\frac {2}{3}}+((4-\pi )/2)^{\frac {2}{3}}}}}}
où
δ
=
α
1
+
α
2
{\displaystyle \delta ={\frac {\alpha }{\sqrt {1+\alpha ^{2}}}}}
γ
^
3
{\displaystyle {\hat {\gamma }}_{3}}
δ
{\displaystyle \delta }
γ
^
3
{\displaystyle {\hat {\gamma }}_{3}}
α
^
=
δ
/
1
−
δ
2
{\displaystyle {\hat {\alpha }}=\delta /{\sqrt {1-\delta ^{2}}}}
Référence (en) A. Azzalini , « A class of distributions which includes the normal ones » , Scand. J. Statist. vol. 12, 1985 , p. 171–178
Article connexe Asymétrie (statistique)
Liens externes
Cet article est issu de
wikipedia . Text licence:
CC BY-SA 4.0 , Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.
















![{\displaystyle \Phi (x)=\int _{-\infty }^{x}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}](https://img.franco.wiki/i/b64168aa76f440a9ab0071082ed917dee8b8a4b6.svg)












