Loi de Nakagami
En théorie des probabilités et en statistique, la loi de Nakagami ou loi de m-Nakagami est une loi de probabilité continue à deux paramètres et de support . Le paramètre est un paramètre de forme, le second paramètre permet de contrôler la propagation. Cette loi est liée à la loi gamma, son nom est issu du statisticien Minoru Nakagami.
| Loi de Nakagami | |
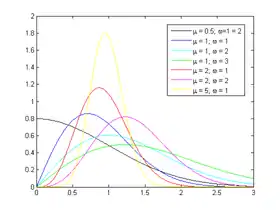 Densité de probabilité | |
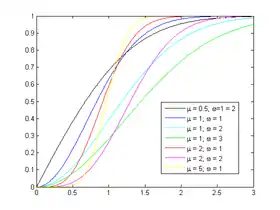 Fonction de répartition | |
| Paramètres | , paramètre de forme , propagation |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | pas d'expression formelle |
| Mode | |
| Variance | |
Caractérisations
La densité de probabilité de la loi de Nakagami est donnée par[1] :
où est la fonction Gamma.
Sa fonction de répartition est :
où P est la fonction gamma incomplète (régularisée).
Simulation
La loi Nakagami est liée à la loi Gamma. En particulier, pour une variable aléatoire Y de loi Gamma, , il est possible d'obtenir une variable aléatoire X de loi de Nakagami, , en posant , , et en considérant la racine carrée de Y :
- .
Historique et applications
L'utilisation de la loi de Nakagami remonte à 1960[3], c'est-à-dire que c'est une loi relativement nouvelle. Elle est utilisée pour modéliser l’atténuation des réseaux sans fils au travers de plusieurs chemins[4].
Références
- (en) Matthias Pätzold, Mobile Radio Channels, Wiley, , 2e éd., 583 p. (ISBN 978-0-470-51747-5, lire en ligne), p. 30
- R. Kolar, R. Jirik, J. Jan (2004) "Estimator Comparison of the Nakagami-m Parameter and Its Application in Echocardiography", Radioengineering, 13 (1), 8–12
- M. Nakagami. "The m-Distribution, a general formula of intensity of rapid fading". In William C. Hoffman, editor, Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium held June 18-20, 1958, pp 3-36. Permagon Press, 1960.
- J. D. Parsons, The Mobile Radio Propagation Channel. New York: Wiley, 1992.















![{\displaystyle m={\frac {\mathbb {E} ^{2}\left[X^{2}\right]}{Var\left[X^{2}\right]}},}](https://img.franco.wiki/i/cf827b7c1aa061548218c348e16d5932f89c1c57.svg)
![{\displaystyle \omega =\mathbb {E} \left[X^{2}\right].}](https://img.franco.wiki/i/f86e4071fa3612bfc1fee1ef5a06772ed12a197a.svg)




