Un lifting en ondelettes est, en mathématiques, un schéma d’implantation d’une transformation en ondelettes un peu différent de celui plus habituel réalisé par les bancs de filtres.
Le lifting en ondelettes est l’expression retenue pour désigner le procédé d’amélioration des propriétés des ondelettes par utilisation réciproque des bandes passe-bas et passe-haut. On obtient ainsi une transformation qui, à partir d’une ondelette à (admettons)  moments nuls, produit une transformée dont les propriétés sont similaires à une ondelette à
moments nuls, produit une transformée dont les propriétés sont similaires à une ondelette à  moments nuls supérieur à
moments nuls supérieur à  .
.
La transformation en ondelettes version lifting est un processus permettant entre autres d’optimiser le nombre d’opérations à exécuter et l’occupation mémoire (le coût de calcul est la moitié du coût de calcul de la FFT !).
Le processus le plus courant pour obtenir une transformation en ondelettes est d’utiliser un banc de filtres (cf. Figure 1), cependant lorsqu’on regarde cette façon de procéder on constate que l’on effectue un sous-échantillonnage par deux après une opération de filtrage : on a donc dépensé en pure perte la moitié du coût de calcul effectué par le filtrage.
L’opération de lifting en ondelettes peut-être vu comme la transformation réalisée par le banc de filtres, mais en intervertissant les phases de filtrage et de sous-échantillonnage. On limite ainsi le nombre d’opérations à effectuer mais, nous perdons en revanche la propriété d’invariance par translation.
Une autre propriété intéressante est que le schéma de lifting est facilement inversible.
Le schéma de lifting est aussi lié aux processus d’échantillonnage et d’interpolation (non explicitement étudié ici) pour la transformation de signaux continus.
On désignera ici par  les coefficients d’ondelettes et par
les coefficients d’ondelettes et par  les coefficients d’échelle obtenus par la transformation.
les coefficients d’échelle obtenus par la transformation.
Pour une ondelette particulière (c.à.d. un couple de filtres  ou
ou  dans l’implémentation par banc de filtres) caractérisée en outre par (disons)
dans l’implémentation par banc de filtres) caractérisée en outre par (disons)  moments nuls (jouant un rôle dans le processus de décroissance des coefficients d’ondelettes à travers les résolutions) pour le filtre primaire et
moments nuls (jouant un rôle dans le processus de décroissance des coefficients d’ondelettes à travers les résolutions) pour le filtre primaire et  moments nuls pour le filtre dual, le schéma d’implantation par lifting permet d’obtenir facilement des ondelettes de moments
moments nuls pour le filtre dual, le schéma d’implantation par lifting permet d’obtenir facilement des ondelettes de moments  et
et  plus élevé. On a donc élevé (lifté) l’ordre de cette ondelette par ce schéma (d’où la justification du nom lifting).
plus élevé. On a donc élevé (lifté) l’ordre de cette ondelette par ce schéma (d’où la justification du nom lifting).
Dans la Figure 1, le signal original  passe par les deux filtres complémentaires
passe par les deux filtres complémentaires ![{\displaystyle \left[\ {\tilde {h}}\ \right]}](https://img.franco.wiki/i/bfd45fb98011954f75d8d70311a6c0c53f3364c7.svg) (passe-bas) et
(passe-bas) et ![{\displaystyle \left[\ {\tilde {g}}\ \right]}](https://img.franco.wiki/i/ecd0fd5960b05259712fa704c5d6a9e582bd6698.svg) (passe-haut), en sortie on peut sous-échantillonner par 2
(passe-haut), en sortie on peut sous-échantillonner par 2 ![{\displaystyle \left[\ \downarrow 2\ \right]}](https://img.franco.wiki/i/2cfee83a4b1deb1bc09efdfd4b4d5618375f146e.svg) et on obtient alors respectivement des coefficients d’ondelettes
et on obtient alors respectivement des coefficients d’ondelettes  et des coefficients d’échelle
et des coefficients d’échelle  .
.
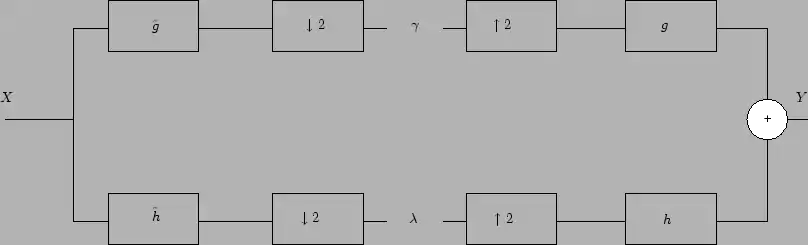
Figure 1
Figure 1. Schéma d’une implémentation en banc de filtres d’une transformation en ondelettes.
La reconstruction du signal s’effectue par sur-échantillonnage par insertion de zéros ![{\displaystyle \left[\ \uparrow 2\ \right]}](https://img.franco.wiki/i/4b514b3e80f569e57068fe5fba68a2aa63430a14.svg) et passage par les filtres de synthèse
et passage par les filtres de synthèse ![{\displaystyle \left[\ h\ \right]}](https://img.franco.wiki/i/5a5661e7d340f32d4da97c74035375346fd5415a.svg) et
et ![{\displaystyle \left[\ g\ \right]}](https://img.franco.wiki/i/5d66b56e4fb33c5c4d302157ad2ceabd991795d8.svg) , puis par simple addition pour obtenir le signal
, puis par simple addition pour obtenir le signal  .
.
On utilisera :
- les ondelettes paresseuses (lazy wavelets) qui servent à séparer un vecteur en composantes paires et impaires,
- ainsi qu’une matrice polyphase qui permet de travailler sélectivement sur les composantes paires ou impaires du signal.
On va factoriser la matrice polyphase et introduire alors deux opérations :
- une opération de prédiction (predict) qui prédit les échantillons de rang pair à partir des échantillons de rang impair ;
- une opération de mise à jour (update) qui permet de conserver sur une partie du signal la valeur moyenne de l’ensemble du signal.
Le formalisme utilisé est celui des articles de références [Sweldens, Valens]. (Attention cependant aux écarts de notations entre les différents articles).
Cette transformation va en outre permettre de réaliser une transformation sur des entiers qui donne des entiers. Cependant il faudra utiliser une étape supplémentaire utilisant aussi le lifting pour la mise à l’échelle.
Vers la réalisation de l’ondelette de Haar version lifting
On part des filtres d’analyse et de reconstruction de l’analyse multi-résolution classique par banc de filtres suivant le schéma classique de la Figure 1 :
![{\displaystyle {\tilde {h}}[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\{\underline {1}}\end{bmatrix}}}](https://img.franco.wiki/i/cf6b14186ac47cf0db31adac3fb8468973ad1499.svg)
![{\displaystyle {\tilde {g}}[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\-{\underline {1}}\end{bmatrix}}}](https://img.franco.wiki/i/a2b03445476badddf1d05ad2af2354c51e355c4a.svg)


![{\displaystyle h[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}{\underline {1}}\\1\end{bmatrix}}}](https://img.franco.wiki/i/be0de192af07647bd9590140ef8ebdc39ef63c9f.svg)
![{\displaystyle g[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}{\underline {1}}\\-1\end{bmatrix}}}](https://img.franco.wiki/i/edb018acb765a5fb835bfc5cd0aedf7ea8137fe3.svg)


Attention aux notations utilisées ci-dessus :
- dans certaines références, on trouve souvent
 et
et  .
.
- dans les expressions des filtres, le coefficient souligné correspond à l’indice
 .
.
Les filtres doivent en outre satisfaire les formules suivantes :


On a besoin de construire la matrice polyphase  ainsi que sa matrice duale
ainsi que sa matrice duale  (le terme polyphase vient de la théorie du filtrage numérique où il est utilisé pour décrire le partitionnement d’une séquence d’échantillons en plusieurs sous-séquences qui peuvent être traitées en parallèle, les sous-séquences peuvent-être vues comme des versions d’elles-mêmes décalées en phase, d’où le nom). On utilise la formule suivante de décomposition polyphase sur les filtres précédents :
(le terme polyphase vient de la théorie du filtrage numérique où il est utilisé pour décrire le partitionnement d’une séquence d’échantillons en plusieurs sous-séquences qui peuvent être traitées en parallèle, les sous-séquences peuvent-être vues comme des versions d’elles-mêmes décalées en phase, d’où le nom). On utilise la formule suivante de décomposition polyphase sur les filtres précédents :
 , où
, où  désigne les échantillons pairs (even) et
désigne les échantillons pairs (even) et  les échantillons impairs (odd) (moyen mnémotechnique : even a un nombre de lettres pair, odd a un nombre de lettres impair).
les échantillons impairs (odd) (moyen mnémotechnique : even a un nombre de lettres pair, odd a un nombre de lettres impair).

Il vient assez facilement :



sachant que  , et que pour
, et que pour  , on a les propriétés suivantes :
, on a les propriétés suivantes :




Ces propriétés montrent que pour passer de l’analyse à la synthèse (de  à
à  , il suffit si
, il suffit si  , de prendre la matrice des cofacteurs en changeant de signe.
, de prendre la matrice des cofacteurs en changeant de signe.
De plus sachant que  (l’inversion temporelle
(l’inversion temporelle  est nécessaire pour compenser le délai introduit par le filtrage) :
est nécessaire pour compenser le délai introduit par le filtrage) :

Lifting primaire
L’élévation primaire (primary lifting) est aussi appelé update. Le lifting à proprement parler consiste à modifier le filtre  en gardant la complémentarité avec
en gardant la complémentarité avec  à l’aide de la formule :
à l’aide de la formule :

où  est un polynôme de Laurent.
est un polynôme de Laurent.
Soit la transformée en Z d’un filtre FIR :
![{\displaystyle h(z)=\sum \limits _{k=p}^{q}h[k]z^{-k}}](https://img.franco.wiki/i/bdfa9d58b9b5064ed96fd0335c89b870a593aa95.svg) .
.
Cette somme est aussi nommée polynôme de Laurent ou encore série de Laurent.
La matrice polyphase devient alors :
 .
.
De la même façon pour  ,
,
 ,
,
où  est un polynôme de Laurent.
est un polynôme de Laurent.
Dès lors,
 .
.
Lifting dual
L’élévation duale (lifting dual) est aussi appelé prédiction.
Les formules précédentes modifient la sous-bande passe-bas à l’aide de la sous-bande passe-haut. Le lifting dual consiste en l’opération inverse : modifier la sous-bande passe-bas à l’aide de la sous-bande passe-haut.
 ,
, ,
,
et
 ,
, ,
,
où  est un polynôme de Laurent.
est un polynôme de Laurent.
On a ainsi élevé (lifté) le niveau de sophistication de la transformation en ondelettes. On a de plus, pour avoir une transformation inversible :
 et
et .
.
Factorisation des filtres
La démarche ici est en quelque sorte la démarche inverse afin de pouvoir passer de forme connue de pairs de filtres d’ondelettes à leur implémentation en termes de lifting d’ondelettes.
On peut réécrire :

en :
 ,
,
qui est une forme de division avec reste (pour réaliser la division avec reste, on utilise l’algorithme d’Euclide) où  est le reste.
est le reste.
Alors :
 .
.
En itérant cet exemple, on peut arriver à obtenir une matrice polyphase qui est de la forme :
 ,
,
où  et
et  sont deux constantes (différentes de zéro) que l’on peut éventuellement factoriser en quatre étapes de lifting.
sont deux constantes (différentes de zéro) que l’on peut éventuellement factoriser en quatre étapes de lifting.

Figure 2
Figure 2. Lifting, chaque voie (sous-bande) est modifiée par l’autre.
On est déjà parti des filtres de la transformation en ondelettes de Haar et on a obtenu la matrice polyphase et sa forme duale. Il reste à factoriser pour avoir l’implémentation en lifting.

Lifting dual
On veut :
 ,
,
 .
.
Par identification, il vient :

Dans notre cas très simple, il n’est pas nécessaire d’utiliser l’algorithme d’Euclide (pour un exemple détaillé de l’utilisation de l’algorithme d’Euclide, voir le cas de l’ondelette de Daubechies D4 ci-après) et on peut prendre
Rappel : soit
 .
.
On applique l’algorithme d’Euclide, soit  .
.
Soient ici :
 , et :
, et : ,
,
où  est l’opérateur modulo et
est l’opérateur modulo et  retourne le quotient entier. La procédure est itérative, plusieurs choix sont en général possible pour le choix de l’ordre du diviseur.
retourne le quotient entier. La procédure est itérative, plusieurs choix sont en général possible pour le choix de l’ordre du diviseur.

 ,
,
d’où :
 .
.
Alors,
 .
.
Lifting primaire
On désire réécrire  sous la forme :
sous la forme :

Par identification, il vient :

On prend :
 et
et  , et
, et
Alors :
 , et
, et .
.
Ces opérations purement matricielles s’implémentent très facilement sous Scilab ou Matlab.
On peut de façon plus condensée (que l’écriture matricielle) écrire le pseudo code pour l’algorithme de calcul in-place :
 et
et  représentent les coefficients pairs et impairs du signal (respectivement),
représentent les coefficients pairs et impairs du signal (respectivement), représente les détails (c.à.d. les coefficients issus du filtrage passe-haut, donc les coefficients d’ondelettes),
représente les détails (c.à.d. les coefficients issus du filtrage passe-haut, donc les coefficients d’ondelettes), représente le signal grossier (smooth) issu du filtrage passe-bas et donc les coefficients d’échelle.
représente le signal grossier (smooth) issu du filtrage passe-bas et donc les coefficients d’échelle.
Alors :

Pour le passage à une résolution supérieure on prend le code précédent que l’on réinitialise en commençant par :
 .
.
La reconstruction se fait en inversant l’ordre des opérations (et leurs signes, sauf pour la normalisation où l’on prend l’inverse).
 .
.
Obtenir des coefficients d’ondelettes entiers peut-être un atout lorsque :
- des valeurs entières sont recommandées (notamment pour les images),
- pour certains processeurs embarqués ne traitant que les entiers,
- l’occupation mémoire est prépondérante (un entier occupe moins de place qu’un flottant).
Lors d’une étape de lifting que l’on a étudié on a utilisé une relation de ce type :

Puisque le signal  n’est pas modifié par cette étape de lifting alors on peut arrondir et réécrire l’étape du lifting.
n’est pas modifié par cette étape de lifting alors on peut arrondir et réécrire l’étape du lifting.

où  note une opération d’arrondi.
note une opération d’arrondi.
Ce qui est très fort, c’est que, quelle que soit l’opération d’arrondi utilisée, la transformation est inversible :

Il y a cependant une précaution à prendre qui concerne la mise à l’échelle (scaling), dans le cas où ces coefficients ne sont pas entiers. La solution dans ce cas consiste à transformer cette mise à l’échelle en 3 étapes supplémentaires de lifting suivant le modèle :
 , ou
, ou
On rappelle :

Pour notre ondelette de Haar, on a un signe différent dans la matrice de normalisation, il suffit juste d’adapter les expressions précédentes avec par exemple pour la première (attention cependant lors de l’inversion) :
 ,
,
avec  .
.
Daubechies(4) signifie que les filtres de cette ondelette possèdent 4 coefficients et  moments nuls. On a aussi :
moments nuls. On a aussi :
 , et
, et .
.
On trouve son expression dans les tables ou dans [Daubechies] :
![{\displaystyle \left\lbrace {\begin{matrix}h_{0}&=&h[0]&=&{\frac {1+{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{1}&=&h[1]&=&{\frac {3+{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{2}&=&h[2]&=&{\frac {3-{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{3}&=&h[3]&=&{\frac {1-{\sqrt {3}}}{4{\sqrt {2}}}}\end{matrix}}\right.}](https://img.franco.wiki/i/b981ecb69adedbfb6addc288eba0e7452b5cf2ea.svg)
On a les propriétés intéressantes suivantes :
 , soit :
, soit :![{\displaystyle \left\lbrace {\begin{matrix}h[0]&=&0,482962913145\\h[1]&=&0,836516303738\\h[2]&=&0,224143868042\\h[3]&=&-0,129409522551\end{matrix}}\right.}](https://img.franco.wiki/i/266a3017db8ce022b7de40468f28d10bd90e4cd7.svg)
 , et
, et

On a alors pour  :
:

 , d’où
, d’où , et
, et
De la même façon pour  :
:

 , et :
, et : .
.
D’où :

Lifting primaire
On va écrire une étape de lifting primaire :

Alors,

On utilise alors la division euclidienne (plusieurs factorisations sont possibles suivant l’ordre dans lequel on choisit de prendre en compte diviseur et dividende) :
Le nombre de possibilités différentes est lié aux degrés (noté  ) des polynômes de Laurent des diviseurs et dividendes. Le degré d’un polynôme de Laurent quelconque
) des polynômes de Laurent des diviseurs et dividendes. Le degré d’un polynôme de Laurent quelconque  défini par :
défini par :
![{\displaystyle h(z)=\sum \limits _{k=p}^{q}h[k]z^{-k}}](https://img.franco.wiki/i/bdfa9d58b9b5064ed96fd0335c89b870a593aa95.svg)
est :  . Soit
. Soit  l’expression de la division euclidienne des polynômes
l’expression de la division euclidienne des polynômes  par
par  , alors
, alors
- si les degrés du diviseur et du dividende sont égaux, alors le nombre de possibilités est
 ,
,
- si maintenant
 , alors le nombre de possibilités est
, alors le nombre de possibilités est  .
.
Par exemple :
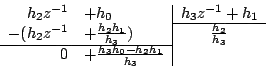
ou alors :
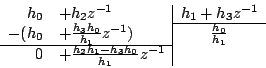
etc.
On se limite à l’exploration de la première solution (les autres aboutiront aussi à des formulations différentes mais équivalentes).
On a alors :
 , et
, et
On explicite alors  :
:
 , d’où
, d’où
Lifting dual
Maintenant, le lifting dual :

Alors,

Effectuons la division euclidienne suivante :
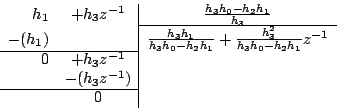 .
.
Donc :
 et
et , alors,
, alors, .
.
Or,
 ,
,
d’où
 .
.
Voilà :

On peut maintenant mettre en évidence la mise à l’échelle d’abord en réécrivant un peu les derniers coefficients obtenus à
l’aide des formules sur les coefficients  :
:
 et
et ,
,
donc,

Mise à l’échelle
On peut donc introduire l’étape de mise à l’échelle (normalisation), en remarquant que :

d’où finalement :
 ,
,
c’est-à-dire :
 , et alors :
, et alors :
Simplification de la mise en œuvre
On peut de façon plus condensée (que l’écriture matricielle) écrire le pseudo-code pour l’algorithme de calcul in situ :
 et
et  représente les coefficients pairs et impairs du signal (respectivement),
représente les coefficients pairs et impairs du signal (respectivement), représente les détails (c.à.d. les coefficients issu du filtrage passe-haut, donc les coefficients d’ondelettes),
représente les détails (c.à.d. les coefficients issu du filtrage passe-haut, donc les coefficients d’ondelettes), représente le signal grossier (smooth) issu du fitlrage passe-bas et donc les coefficients d’échelle.
représente le signal grossier (smooth) issu du fitlrage passe-bas et donc les coefficients d’échelle.
![{\displaystyle {\begin{matrix}s&=&x_{o}+{\sqrt {3}}x_{e};\\d&=&x_{e}-{\sqrt {3}}/4*s-({\sqrt {3}}-2)/4*[0\ s(1:1:length(s)-1)];\\s&=&s-[d(2:1:length(d))\ 0];\\d&=&({\sqrt {3}}+1)/{\sqrt {2}}*d;\\s&=&({\sqrt {3}}-1)/{\sqrt {2}}*s;\end{matrix}}}](https://img.franco.wiki/i/b73defa2d7847c5994e4e7b4481b57418a82319e.svg)
Pour le passage à une résolution supérieure, on prend le code précédent que l’on réinitialise en commençant par :

L’implémentation peut se faire facilement suivant l’exemple de la Figure 8.
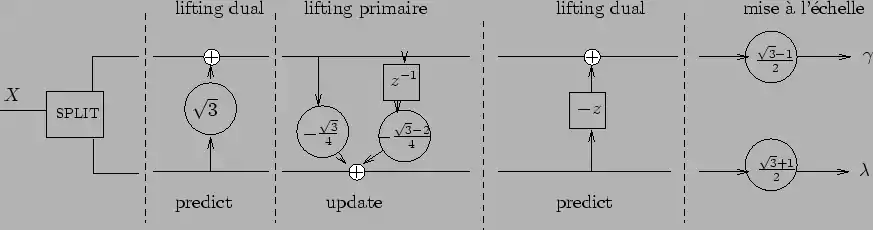
Figure 8
Figure 8. Schéma d’une implémentation du lifting


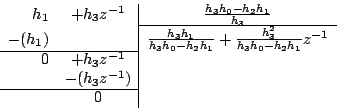 .
.







![{\displaystyle \left[\ {\tilde {h}}\ \right]}](https://img.franco.wiki/i/bfd45fb98011954f75d8d70311a6c0c53f3364c7.svg)
![{\displaystyle \left[\ {\tilde {g}}\ \right]}](https://img.franco.wiki/i/ecd0fd5960b05259712fa704c5d6a9e582bd6698.svg)
![{\displaystyle \left[\ \downarrow 2\ \right]}](https://img.franco.wiki/i/2cfee83a4b1deb1bc09efdfd4b4d5618375f146e.svg)


![{\displaystyle \left[\ \uparrow 2\ \right]}](https://img.franco.wiki/i/4b514b3e80f569e57068fe5fba68a2aa63430a14.svg)
![{\displaystyle \left[\ h\ \right]}](https://img.franco.wiki/i/5a5661e7d340f32d4da97c74035375346fd5415a.svg)
![{\displaystyle \left[\ g\ \right]}](https://img.franco.wiki/i/5d66b56e4fb33c5c4d302157ad2ceabd991795d8.svg)

![{\displaystyle {\tilde {h}}[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\{\underline {1}}\end{bmatrix}}}](https://img.franco.wiki/i/cf6b14186ac47cf0db31adac3fb8468973ad1499.svg)
![{\displaystyle {\tilde {g}}[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1\\-{\underline {1}}\end{bmatrix}}}](https://img.franco.wiki/i/a2b03445476badddf1d05ad2af2354c51e355c4a.svg)


![{\displaystyle h[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}{\underline {1}}\\1\end{bmatrix}}}](https://img.franco.wiki/i/be0de192af07647bd9590140ef8ebdc39ef63c9f.svg)
![{\displaystyle g[n]={\frac {1}{\sqrt {2}}}{\begin{bmatrix}{\underline {1}}\\-1\end{bmatrix}}}](https://img.franco.wiki/i/edb018acb765a5fb835bfc5cd0aedf7ea8137fe3.svg)































![{\displaystyle h(z)=\sum \limits _{k=p}^{q}h[k]z^{-k}}](https://img.franco.wiki/i/bdfa9d58b9b5064ed96fd0335c89b870a593aa95.svg)


























































![{\displaystyle \left\lbrace {\begin{matrix}h_{0}&=&h[0]&=&{\frac {1+{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{1}&=&h[1]&=&{\frac {3+{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{2}&=&h[2]&=&{\frac {3-{\sqrt {3}}}{4{\sqrt {2}}}}\\h_{3}&=&h[3]&=&{\frac {1-{\sqrt {3}}}{4{\sqrt {2}}}}\end{matrix}}\right.}](https://img.franco.wiki/i/b981ecb69adedbfb6addc288eba0e7452b5cf2ea.svg)

![{\displaystyle \left\lbrace {\begin{matrix}h[0]&=&0,482962913145\\h[1]&=&0,836516303738\\h[2]&=&0,224143868042\\h[3]&=&-0,129409522551\end{matrix}}\right.}](https://img.franco.wiki/i/266a3017db8ce022b7de40468f28d10bd90e4cd7.svg)






















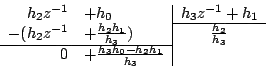
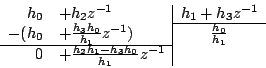





















![{\displaystyle {\begin{matrix}s&=&x_{o}+{\sqrt {3}}x_{e};\\d&=&x_{e}-{\sqrt {3}}/4*s-({\sqrt {3}}-2)/4*[0\ s(1:1:length(s)-1)];\\s&=&s-[d(2:1:length(d))\ 0];\\d&=&({\sqrt {3}}+1)/{\sqrt {2}}*d;\\s&=&({\sqrt {3}}-1)/{\sqrt {2}}*s;\end{matrix}}}](https://img.franco.wiki/i/b73defa2d7847c5994e4e7b4481b57418a82319e.svg)